Test: Greedy Techniques- 2 - Computer Science Engineering (CSE) MCQ
20 Questions MCQ Test - Test: Greedy Techniques- 2
Let G be an undirected connected graph with distinct edge weight. Let emax be the edge with maximum weight and emin the edge with minimum weight. Which of the following statements is false?
Which of the following algorithm can be used to efficiently calculate single source shortest paths in a Directed Acyclic Graph?
Consider the undirected graph below:
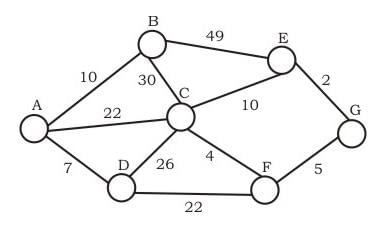
Using Prim's algorithm to construct a minimum spanning tree starting with node A, which one of the following sequences of edges represents a possible order in which the edges would be added to construct the minimum spanning tree?

Consider the following graph:
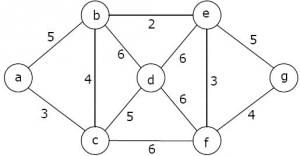
Which one of the following is NOT the sequence of edges added to the minimum spanning tree using Kruskal's algorithm?
Given a directed graph where weight of every edge is same, we can efficiently find shortest path from a given source to destination using?
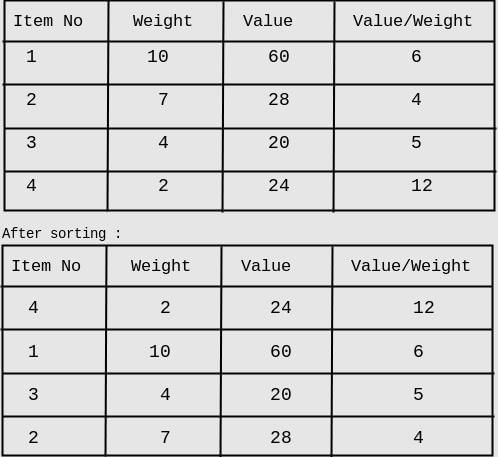
Consider the weights and values of items listed below. Note that there is only one unit of each item.
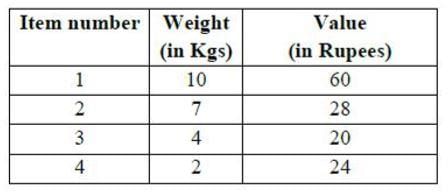
The task is to pick a subset of these items such that their total weight is no more than 11 Kgs and their total value is maximized. Moreover, no item may be split. The total value of items picked by an optimal algorithm is denoted by Vopt. A greedy algorithm sorts the items by their value-to-weight ratios in descending order and packs them greedily, starting from the first item in the ordered list. The total value of items picked by the greedy algorithm is denoted by Vgreedy. The value of Vopt − Vgreedy is ______ .
Note -This was Numerical Type question.
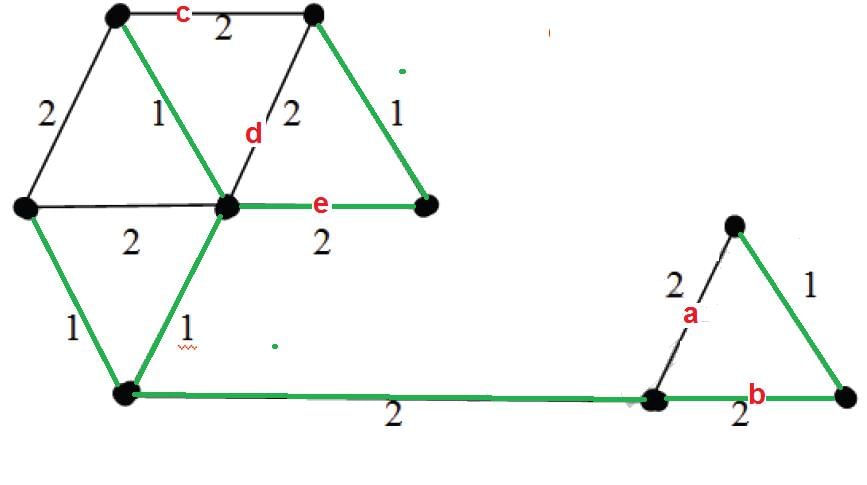
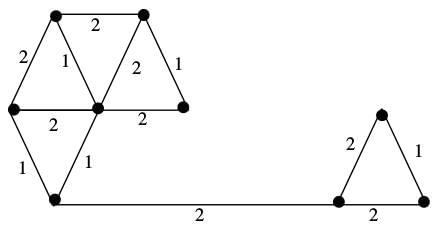
The number of distinct minimum spanning trees for the weighted graph below is ____
Is the following statement valid about shortest paths? Given a graph, suppose we have calculated shortest path from a source to all other vertices. If we modify the graph such that weights of all edges is becomes double of the original weight, then the shortest path remains same only the total weight of path changes.
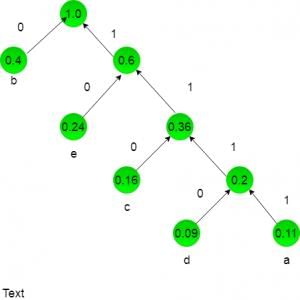
A text is made up of the characters a, b, c, d, e each occurring with the probability 0.11, 0.40, 0.16, 0.09 and 0.24 respectively. The optimal Huffman coding technique will have the average length of:
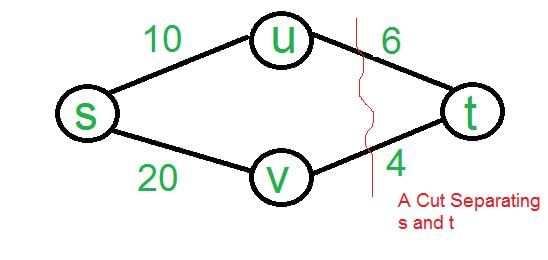
Let s and t be two vertices in a undirected graph G + (V, E) having distinct positive edge weights. Let [X, Y] be a partition of V such that s ∈ X and t ∈ Y. Consider the edge e having the minimum weight amongst all those edges that have one vertex in X and one vertex in Y The edge e must definitely belong to:
Given a weighted graph where weights of all edges are unique (no two edge have same weights), there is always a unique shortest path from a source to destination in such a graph.
Six files F1, F2, F3, F4, F5 and F6 have 100, 200, 50, 80, 120, 150 records respectively. In what order should they be stored so as to optimize act. Assume each file is accessed with the same frequency
What is the weight of a minimum spanning tree of the following graph ?
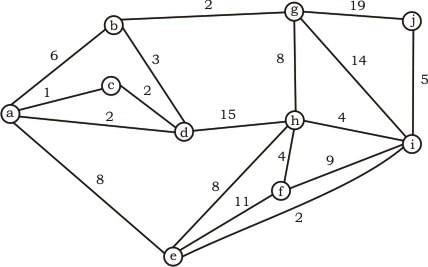
Which of the following statement(s)is / are correct regarding Bellman-Ford shortest path algorithm?
P: Always finds a negative weighted cycle, if one exist s.
Q: Finds whether any negative weighted cycle is reachable from the source.
The number of permutations of the characters in LILAC so that no character appears in its original position, if the two L’s are indistinguishable, is ________ . Note - This question was Numerical Type.
Consider an undirected unweighted graph G. Let a breadth-first traversal of G be done starting from a node r. Let d(r,u) and d(r,v) be the lengths of the shortest paths from r to u and v respectively in G. If u is visited before v during the breadth-first traversal, which of the following statements is correct?
Let G = (V, E) be an undirected graph with a subgraph G1 = (V1, El). Weights are assigned to edges of G as follows :
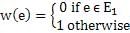
A single-source shortest path algorithm is executed on the weighted graph (V, E, w) with an arbitrary vertex ν1 of V1 as the source. Which of the following can always be inferred from the path costs computed?
Define Rn to be the maximum amount earned by cutting a rod of length n meters into one or more pieces of integer length and selling them. For i>0, let p[i] denote the selling price of a rod whose length is i meters. Consider the array of prices:
p[1]=1, p[2]=5, p[3]=8, p[4]=9, p[5]=10, p[6]=17, p[7]=18
Which of the following statements is/are correct about R7?
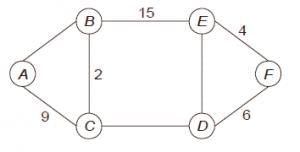
The graph shown below 8 edges with distinct integer edge weights. The minimum spanning tree (MST) is of weight 36 and contains the edges: {(A, C), (B, C), (B, E), (E, F), (D, F)}. The edge weights of only those edges which are in the MST are given in the figure shown below. The minimum possible sum of weights of all 8 edges of this graph is ______________.
Let G = (V, E) be a simple undirected graph, and s be a particular vertex in it called the source. For x ∈ V, let d(x) denote the shortest distance in G from s to x. A breadth first search (BFS) is performed starting at s. Let T be the resultant BFS tree. If (u, v) is an edge of G that is not in T, then which one of the following CANNOT be the value of d(u) – d(v)?