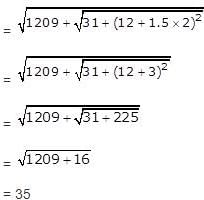RRB JE EEE (CBT I) Mock Test- 10 - Electrical Engineering (EE) MCQ
30 Questions MCQ Test - RRB JE EEE (CBT I) Mock Test- 10
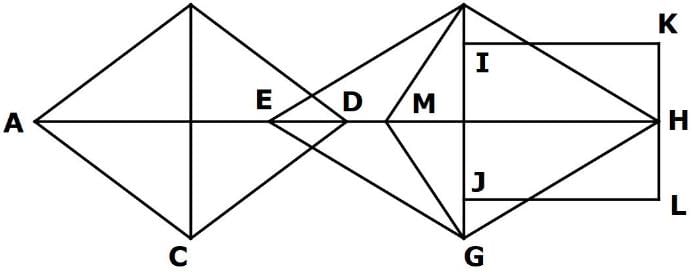
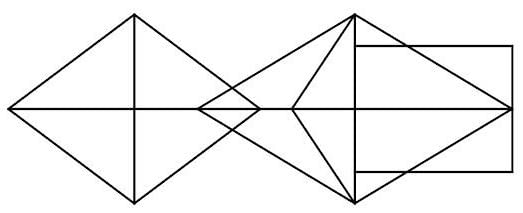
Find the minimum number of straight lines to make the given figure.

If 1.96 of 1.2 of a = 3.43 of 1.6 of b. Find b: a.
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Following bar graph shows the sales of clothes of 3 Brands: Levi's, Lee Cooper and Spykar in Central Mall in Bangalore for the months of October, November and December.
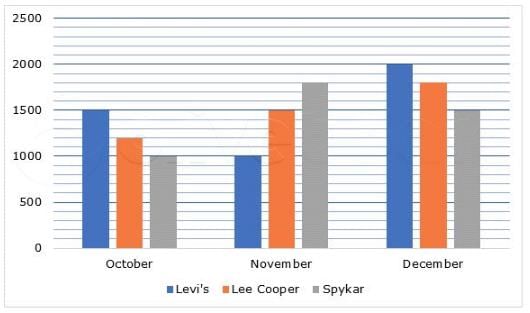
For all 3 months, what is the difference between the sum of the number of Levi's and Spykar clothes sold and the number of Lee Cooper clothes sold?

What will come in place of (?) in this equation?
? ÷ [(5/12) of (12/25) of 125 ÷ {√(21 + √16)/2}] = ? + 3
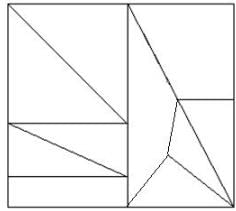
How many triangles are present in the given figure?
Calculate the difference between mean deviation and variance of given numbers.
3, 6, 8, 1, 4, 6, 4, 2, 2, 4
What value we get if divide (11/5) + (9/4) + (7/2) by (132 - 10)?
A Faulty watch gains 1 hour in 6 hours. After how many days will it show the correct time again?
If, it is given that, 82 - 28 = 32 and 65 - 42 = 38, then, 76 - 18 = ?
If a quadratic equation 3x2 - 4√3x + m = 0 has equal roots, then find the value of 3m2 - 5m + 16.
How many numbers are irrational among the numbers given below?
6th root of 2187, 5th root of 4096, √(28 x 23 - 283), √(34 x 35 - 23 x 22), √4802
A contractor undertakes to complete a work in 19 weeks. He employs 180 men for 7 weeks and they complete 1/2 of the work. He then reduces the number of men to 140, who work for 5 weeks. How many men must be employed for the remaining period to finish the work?
A man bought six different fruits, and, each fruit's quantity bought is different. Quantity of Papaya bought is less than that of Oranges as well as Mango. Quantity of Apples bought is less than both Kiwi and Banana. Quantity of Mango is more than only one fruits and that of oranges is more than at least two fruits. Apple's quantity is more than that of oranges. Which fruit's quantity is less than that of three fruits?
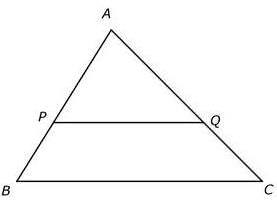
In ∆ABC, P and Q are points on AB and AC respectively such that AP:PB = 2:1 and AQ:QC = 2:1. If BC = 18 cm, what is the length of PQ?
The Pie-Chart shows the percentage distribution of the number of employees that work in a particular department within a Company.
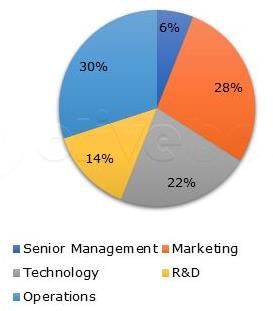
If the number of employees that work in R&D is 588, what is the number of employees who work in Senior Management?
Area of a circle is 706.5 cm2 and its radius is increased by a certain amount so that its circumference is increased by 31.4 cm. What is the new area of the circle? (Use π = 3.14)
What is the angle between the initial and final position of the second hand of o watch when it has travelled from 02:37:42 p.m. to 02:39:54 p.m.?
A person has total of Rs.60000 with him, out which 60% he invested in scheme A at 15% SI for 4 years and remaining in scheme B at 25% SI for 4 years. Now, total interest after 4 years he invested in scheme B for 2 years and total principle amount he invested in scheme A for 2 years. What will be the difference between total amount of interest from both the schemes after 6 years?
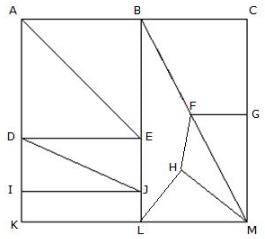
Given below are the steps involved. Arrange them in the sequential order.
(A) Amount invested in scheme A and scheme B for the second time is Rs.60000 and [21600 + 24000 = Rs.45600] respectively.
(B) Required difference = (21600 + 18000) ~ (24000 + 22800) = Rs.7200
(C) Initial amount invested in scheme A and B is 60% of 60000 = Rs.36000 and 40% of 60000 = Rs.24000 respectively.
(D) Interest from scheme A and scheme B after 2 years = [(60000 * 15 * 2)/100 = Rs.18000] and [(45600 * 25 * 2)/100 = Rs.22800] respectively.
(E) Interest from scheme A and scheme B after 4 years = [(36000 * 15 * 4)/100 = Rs.21600] and [(24000 * 25 * 4)/100 = Rs.24000] respectively.
A is as much younger than B as he is older than C. If the sum of the ages of B and C is 15 years, what is definitely the difference between B and A's age?
What is the value of (2/3) of (6/7) of (14/15) of [63 ÷ {√625 − √(80 ÷ √(100 ÷ 8 X 2))}]?
The product of three numbers a, b and 21 is 10290 and their HCF is 7. If a is greater than b and b is greater than 10, then find the LCM of greatest and smallest number.
Find the value of 13 + (1/3) of 81 - (1/4) of 192 + 23 of 16 ÷ 92.
By selling 45 sweets for Rs 40 a man losses 20%. How much should he sell for Rs 24 to gain 20%?
A shopkeeper has 5 items such that their mean weight is 30 kg. If weight of these items are consecutive multiples of 5, what will be the sum of the weight of the lightest and heaviest item?
Ram had Rs 2000, part of which he lent at 15% for two years at simple interest and the rest at 10% at compound interest for two years. The total interest was Rs 528. Find the sum lent at simple interest (in Rs)?