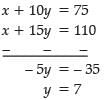All Courses
Get the App Signup / Login
Sign in Open App
Class 9 Exam  >  Class 9 Tests  >  Case Based Questions Test: Pair of Linear Equations in Two Variables - Class 9 MCQ

Case Based Questions Test: Pair of Linear Equations in Two Variables - Class 9 MCQ


Test Description

12 Questions MCQ Test - Case Based Questions Test: Pair of Linear Equations in Two Variables

Case Based Questions Test: Pair of Linear Equations in Two Variables for Class 9 2024 is part of Class 9 preparation. The Case Based Questions Test: Pair of Linear Equations in Two Variables questions and answers have been prepared according to the Class 9 exam syllabus.The Case Based Questions Test: Pair of Linear Equations in Two Variables MCQs are made for Class 9 2024 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests for Case Based Questions Test: Pair of Linear Equations in Two Variables below.
Solutions of Case Based Questions Test: Pair of Linear Equations in Two Variables questions in English are available as part of our course for Class 9 & Case Based Questions Test: Pair of Linear Equations in Two Variables solutions in Hindi for Class 9 course. Download more important topics, notes, lectures and mock test series for Class 9 Exam by signing up for free. Attempt Case Based Questions Test: Pair of Linear Equations in Two Variables | 12 questions in 24 minutes | Mock test for Class 9 preparation | Free important questions MCQ to study for Class 9 Exam | Download free PDF with solutions
Case Based Questions Test: Pair of Linear Equations in Two Variables - Question 1
Save

Direction: Read the following text and answer the following questions on the basis of the same:

Places A and B are 100 km apart on a highway. One car starts from A and another from B at the same time. If the cars travel in the same direction at different speeds, they meet in 5 hours. If they travel towards each other, they meet in 1 hour.

The given problem is based on which mathematical concept

Detailed Solution for Case Based Questions Test: Pair of Linear Equations in Two Variables - Question 1
The given problem is based on pair of linear equations.
Case Based Questions Test: Pair of Linear Equations in Two Variables - Question 2
Save

Direction: Read the following text and answer the following questions on the basis of the same:

Places A and B are 100 km apart on a highway. One car starts from A and another from B at the same time. If the cars travel in the same direction at different speeds, they meet in 5 hours. If they travel towards each other, they meet in 1 hour.

What is the relative speed of both cars while they are travelling towards each other ?

Detailed Solution for Case Based Questions Test: Pair of Linear Equations in Two Variables - Question 2
Relative speed of both cars while they are travelling in opposite directions i.e., travelling towards each other = (u + v) km/hr.
1 Crore+ students have signed up on EduRev. Have you? Download the App
Case Based Questions Test: Pair of Linear Equations in Two Variables - Question 3
Save

Direction: Read the following text and answer the following questions on the basis of the same:

Places A and B are 100 km apart on a highway. One car starts from A and another from B at the same time. If the cars travel in the same direction at different speeds, they meet in 5 hours. If they travel towards each other, they meet in 1 hour.

Q. What are the speeds of the two cars?

Detailed Solution for Case Based Questions Test: Pair of Linear Equations in Two Variables - Question 3


Case Based Questions Test: Pair of Linear Equations in Two Variables - Question 4
Save

Direction: Read the following text and answer the following questions on the basis of the same:

Places A and B are 100 km apart on a highway. One car starts from A and another from B at the same time. If the cars travel in the same direction at different speeds, they meet in 5 hours. If they travel towards each other, they meet in 1 hour.

Assuming that the speed of first car and second car be u km/h and v km/h respectively.

What is the relative speed of both cars while they are travelling in the same direction ?
Detailed Solution for Case Based Questions Test: Pair of Linear Equations in Two Variables - Question 4
Relative speed of both cars while they are travelling in same direction = (u – v) km/hr.
Case Based Questions Test: Pair of Linear Equations in Two Variables - Question 5
Save

Direction: Read the following text and answer the following questions on the basis of the same:

Places A and B are 100 km apart on a highway. One car starts from A and another from B at the same time. If the cars travel in the same direction at different speeds, they meet in 5 hours. If they travel towards each other, they meet in 1 hour. What is the difference of speeds in Km/hr of the two cars?
Detailed Solution for Case Based Questions Test: Pair of Linear Equations in Two Variables - Question 5

Let the speed of car at A be x kmph

and the speed of car at B be y kmph

 

when the car travel in same direction Relative Speed is x−y

Dist=100km

t=5 hours

∴  Dist =S×T

100=(x−y)5

x−y=20⟶(I)

 

when car travel in opp direction Relative Speed is x+y

Dist=100km

t=1 hours

Dist=ST

100=(x+y)1

x+y=100⟶(II)

 

Solving (I) & (II)

x−y=20

x+y=100​

   2x=120

x=60km/h

y=40km/h

 

Speed of the car at A =60 km/h

Speed of the car at B=40 km/h

The difference of speeds is 60−40=20

Case Based Questions Test: Pair of Linear Equations in Two Variables - Question 6
Save

Direction: Read the following text and answer the following questions on the basis of the same:

It is common that Governments revise travel fares from time to time based on various factors such as inflation (a general increase in prices and fall in the purchasing value of money) on different types of vehicles like auto, Rickshaws, taxis, Radio cab etc. The auto charges in a city comprise of a fixed charge together with the charge for the distance covered. Study the following situations.

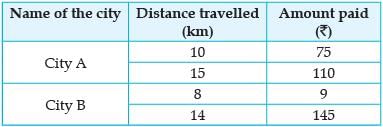
Situation 2: In a city B, for a journey of 8 km, the charge paid is ₹ 91 and for a journey of 14 km, the charge paid is ₹ 145.

The graph of lines representing the conditions are:
Detailed Solution for Case Based Questions Test: Pair of Linear Equations in Two Variables - Question 6
For situation 2, the lines are

p + 8q = 91

p + 14q = 145

There is not graph which matches both lines.

Case Based Questions Test: Pair of Linear Equations in Two Variables - Question 7
Save

Direction: Read the following text and answer the following questions on the basis of the same:

It is common that Governments revise travel fares from time to time based on various factors such as inflation (a general increase in prices and fall in the purchasing value of money) on different types of vehicles like auto, Rickshaws, taxis, Radio cab etc. The auto charges in a city comprise of a fixed charge together with the charge for the distance covered. Study the following situations.

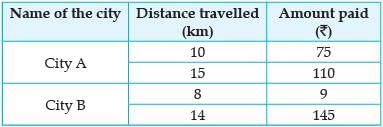
Situation 2: In a city B, for a journey of 8 km, the charge paid is ₹ 91 and for a journey of 14 km, the charge paid is ₹ 145.

What will a person have to pay for travelling a distance of 30 km?
Detailed Solution for Case Based Questions Test: Pair of Linear Equations in Two Variables - Question 7
Let fixed charge be Rs x and running charges be Rs y

For the journey of 8km is paid Rs 91

x + 8y = 91

For the journey of 14km the charge paid is Rs145

x + 14y = 145

Using substitution method

we get,

x = 19

y = 9

ATQ,

If a person travels 30km

Total charged = fixed charges + running charges * 30

= 19 + 30 * 9

= 19 + 210

= Rs 289

Case Based Questions Test: Pair of Linear Equations in Two Variables - Question 8
Save

Direction: Read the following text and answer the following questions on the basis of the same:

It is common that Governments revise travel fares from time to time based on various factors such as inflation (a general increase in prices and fall in the purchasing value of money) on different types of vehicles like auto, Rickshaws, taxis, Radio cab etc. The auto charges in a city comprise of a fixed charge together with the charge for the distance covered. Study the following situations.

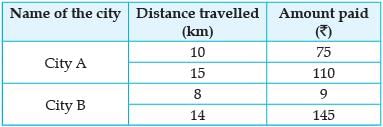
Situation 1: In city A, for a journey of 10 km, the charge paid is ₹ 75 and for a journey of 15 km, the charge paid is ₹ 110.

If the fixed charges of auto rickshaw be ₹ x and the running charges be ₹ y km/hr, the pair of linear equations representing the situation is
Detailed Solution for Case Based Questions Test: Pair of Linear Equations in Two Variables - Question 8
According to given situation, we have

x + 10y = 75 ...(i)

x + 15y = 110 ...(ii)

Case Based Questions Test: Pair of Linear Equations in Two Variables - Question 9
Save

Direction: Read the following text and answer the following questions on the basis of the same:

It is common that Governments revise travel fares from time to time based on various factors such as inflation (a general increase in prices and fall in the purchasing value of money) on different types of vehicles like auto, Rickshaws, taxis, Radio cab etc. The auto charges in a city comprise of a fixed charge together with the charge for the distance covered. Study the following situations.

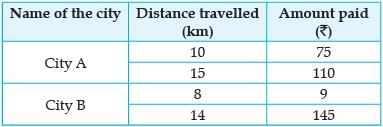
Situation 1: In city A, for a journey of 10 km, the charge paid is ₹ 75 and for a journey of 15 km, the charge paid is ₹ 110.

A person travels a distance of 50 km. The amount he has to pay is
Detailed Solution for Case Based Questions Test: Pair of Linear Equations in Two Variables - Question 9
Solving two equations,

Now, putting y = 7 in equation (i)

x + 10 × 7 = 75

x + 70 = 75

x = 75 – 70

x = 5

Now, if a person travels a distance of 50 km then, amount = x + 50y

= 5 + 50 × 7

= 5 + 350

= 355

Case Based Questions Test: Pair of Linear Equations in Two Variables - Question 10
Save

Direction: Read the following text and answer the following questions on the basis of the same:

John and Jivanti are playing with the marbles in the playground. They together have 45 marbles and John has 15 marbles more than Jivanti.

The given problem is based on which mathematical concept ?
Detailed Solution for Case Based Questions Test: Pair of Linear Equations in Two Variables - Question 10
The given problem is based on pair of linear equations.
Case Based Questions Test: Pair of Linear Equations in Two Variables - Question 11
Save

Direction: Read the following text and answer the following questions on the basis of the same:

John and Jivanti are playing with the marbles in the playground. They together have 45 marbles and John has 15 marbles more than Jivanti.

The number of marbles John had:
Detailed Solution for Case Based Questions Test: Pair of Linear Equations in Two Variables - Question 11
According to the solution of question 1, we get x = 30.
Case Based Questions Test: Pair of Linear Equations in Two Variables - Question 12
Save

John and Jivanti together have 45 marbles. Both of them lost 5 marbles each, and the product of the number of marbles they now have is 124. From the quadratic equation to find how many marbles they had to start with, if John had x marbles.
Detailed Solution for Case Based Questions Test: Pair of Linear Equations in Two Variables - Question 12

Given John and Jivanti together have 45 marbles

 

Let the number of Marbles John had be =x

 

Then the number of marbles Jivanti had=45−x

 

Both of them lost 5 Marbles each

Therefore, the number of marbles John had=x−5

 

The number of marbles Jivanti had=45−x−5=40−x

 

Now product of the number of Marbles =124

∴(x−5)(40−x)=124

 

40x−x²−200+5x=124

 

−x²+45x−200−124=0

 

x²−45x+328=0 --- (Multiplying by(-1))

 

By factorization method

 

x2−36x−9x+324=0

x(x−36)−9(x−36)=0

(x−36)(x−9)=0

 

x=36 or x=9

 

When John has 36 Marbles, Jivanti has =45−x=45−36=9 marbles

 

When John has 9 Marbles and Jivanti has =45−x=45−9=36 marbles

Information about Case Based Questions Test: Pair of Linear Equations in Two Variables Page
In this test you can find the Exam questions for Case Based Questions Test: Pair of Linear Equations in Two Variables solved & explained in the simplest way possible. Besides giving Questions and answers for Case Based Questions Test: Pair of Linear Equations in Two Variables, EduRev gives you an ample number of Online tests for practice

Top Courses for Class 9

Download as PDF

Top Courses for Class 9

Important Questions for Case Based Questions Test: Pair of Linear Equations in Two Variables

Find all the important questions for Case Based Questions Test: Pair of Linear Equations in Two Variables at EduRev.Get fully prepared for Case Based Questions Test: Pair of Linear Equations in Two Variables with EduRev's comprehensive question bank and test resources. Our platform offers a diverse range of question papers covering various topics within the Case Based Questions Test: Pair of Linear Equations in Two Variables syllabus. Whether you need to review specific subjects or assess your overall readiness, EduRev has you covered. The questions are designed to challenge you and help you gain confidence in tackling the actual exam. Maximize your chances of success by utilizing EduRev's extensive collection of Case Based Questions Test: Pair of Linear Equations in Two Variables resources.

Case Based Questions Test: Pair of Linear Equations in Two Variables MCQs with Answers

Prepare for the Case Based Questions Test: Pair of Linear Equations in Two Variables within the Class 9 exam with comprehensive MCQs and answers at EduRev. Our platform offers a wide range of practice papers, question papers, and mock tests to familiarize you with the exam pattern and syllabus. Access the best books, study materials, and notes curated by toppers to enhance your preparation. Stay updated with the exam date and receive expert preparation tips and paper analysis. Visit EduRev's official website today and access a wealth of videos and coaching resources to excel in your exam.

Online Tests for Case Based Questions Test: Pair of Linear Equations in Two Variables

Practice with a wide array of question papers that follow the exam pattern and syllabus. Our platform offers a user-friendly interface, allowing you to track your progress and identify areas for improvement. Access detailed solutions and explanations for each test to enhance your understanding of concepts. With EduRev's Online Tests, you can build confidence, boost your performance, and ace Case Based Questions Test: Pair of Linear Equations in Two Variables with ease. Join thousands of successful students who have benefited from our trusted online resources.
© EduRev
Education Revolution
Follow Us
Signup to see your scores go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup