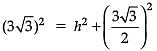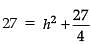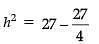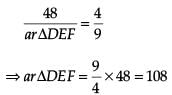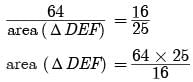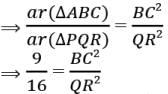All Courses
Get the App Signup / Login
Sign in Open App
Grade 10 Exam  >  Grade 10 Tests  >  Assertion & Reason Test: Triangles - Grade 10 MCQ

Assertion & Reason Test: Triangles - Grade 10 MCQ


Test Description

10 Questions MCQ Test - Assertion & Reason Test: Triangles

Assertion & Reason Test: Triangles for Grade 10 2024 is part of Grade 10 preparation. The Assertion & Reason Test: Triangles questions and answers have been prepared according to the Grade 10 exam syllabus.The Assertion & Reason Test: Triangles MCQs are made for Grade 10 2024 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests for Assertion & Reason Test: Triangles below.
Solutions of Assertion & Reason Test: Triangles questions in English are available as part of our course for Grade 10 & Assertion & Reason Test: Triangles solutions in Hindi for Grade 10 course. Download more important topics, notes, lectures and mock test series for Grade 10 Exam by signing up for free. Attempt Assertion & Reason Test: Triangles | 10 questions in 20 minutes | Mock test for Grade 10 preparation | Free important questions MCQ to study for Grade 10 Exam | Download free PDF with solutions
Assertion & Reason Test: Triangles - Question 1
Save

Direction: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.

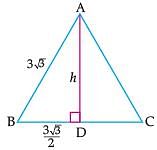
Assertion (A): In an equilateral triangle of side 3√3 cm, then the length of the altitude is 4.5 cm.

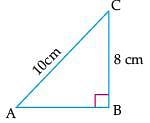
Reason (R): If a ladder 10 cm long reaches a window 8 cm above the ground, then the distance of the foot of the ladder from the base of the wall is 6 cm.

Detailed Solution for Assertion & Reason Test: Triangles - Question 1

In case of assertion

ΔABD, ∠D = 90°

or

or

or, h2 = 81/4

∴ h = 9/2 = 4.5 m

∴ Assertion is correct.

In case of reason: Let BC be the height of the window above the ground and AC be a ladder.

Here, BC = 8 cm and AC = 10 cm

∴ In right angled triangle ABC, AC2 = AB2 + BC2

(By using Pythagoras Theorem)

⇒ (10)2 = AB2 + (8)2

⇒ AB2 = 100 – 64

= 36

⇒ AB = 6 cm.

∴ Reason is correct.

Hence, both assertion and reason are correct but reason is not the correct explanation for assertion.

Assertion & Reason Test: Triangles - Question 2
Save

Direction: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.

Assertion : In the ΔABC , AB = 24 cm , BC = 10 cm and AC = 26 cm , then ΔABC is a right angle triangle.

Reason : If in two triangles, their corresponding angles are equal, then the triangles are similar.

Detailed Solution for Assertion & Reason Test: Triangles - Question 2
We have, AB2 + BC2 = (24)2 + (10)2

= 576 + 100 = 676 = 2

AB2 + BC2 = AC2

ABC is a right angled triangle.

Also, two triangle are similar if their corresponding angles are equal.

So, both A and R are correct but R does not explain A.

1 Crore+ students have signed up on EduRev. Have you? Download the App
Assertion & Reason Test: Triangles - Question 3
Save

Direction: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.

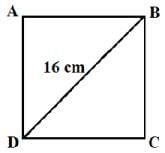
Assertion : The length of the side of a square whose diagonal is 16 cm, is 8√2 cm

Reason : In a right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.

Detailed Solution for Assertion & Reason Test: Triangles - Question 3
We know that In a right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides. This is Pythagoras theorem. So, Reason is correct

Let the side of square be x cm.

In ∆ABD, by Pythagoras theorem, we have BD2 = AB2 + AD2

⇒ 162 = x2 + x2

⇒ 2x2 = 256 ⇒ x2 = 128 ⇒ x = 8√2 cm

So, Assertion is also correct.

Assertion & Reason Test: Triangles - Question 4
Save

Direction: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.

Assertion (A): Corresponding sides of two similar triangles are in the ratio of 2 : 3. If the area of the smaller triangle is 48 cm2, then the area of the larger triangle is 108 cm2.

Reason (R): If D is a point on the side BC of a triangle ABC such that ∠ADC = ∠BAC, then CA2 = CB × CD.
Detailed Solution for Assertion & Reason Test: Triangles - Question 4
In case of assertion

Let ΔABC and ΔDEF are two similar triangles.

Given that ar ΔABC = 48 cm2. Then,

Thus, the area of larger triangle is 108 cm2.

∴ Assertion is correct.

In case of reason:

In ΔBAC and ΔADC,

∠BAC= ∠ADC [Given]

∠BCA= ∠ACD [Common angle]

By AA similarity, ΔBAC ~ ΔADC

Thus,

CA/CD = BC/CA

∴ Reason is correct.

Hence, both assertion and reason are correct but reason is not the correct explanation for assertion.

Assertion & Reason Test: Triangles - Question 5
Save

Direction: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.

Assertion : ABC and DEF are two similar triangles such that BC = 4 cm , EF = 5 cm and area of ΔABC = 64 cm2 , then area of ΔDEF = 100 cm2.

Reason : The areas of two similar triangles are in the ratio of the squares of teh corresponding altitudes.
Detailed Solution for Assertion & Reason Test: Triangles - Question 5
Reason is true. [standard result]

For Assertion, since ΔABC ∼ ΔDEF

(ratio of areas of two similar Δs is equal to the ratio of the squares of corresponding sides)

= 4 x 25 = 100 cm2

Assertion is true. But Reason is not correct explanation for Assertion.

Assertion & Reason Test: Triangles - Question 6
Save

Direction: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.

Assertion : The areas of two similar triangles ABC and PQR are in the ratio 9 :16. If BC = 4.5 cm, then the length of QR is 6 cm.

Reason : The ratio of the areas of two similar triangles is equal to the ratio of their corresponding sides.
Detailed Solution for Assertion & Reason Test: Triangles - Question 6
We know that the ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides.

So, Reason is not correct

So, Assertion is correct

Assertion & Reason Test: Triangles - Question 7
Save

Direction: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.

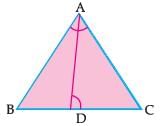
Assertion (A): If D is a point on side QR of ΔPQR such that PD ⊥ QR, then ΔPQD ~ ΔRPD.

Reason (R): In the figure given below, if ∠D = ∠C then ΔADE ~ ΔACB.
Detailed Solution for Assertion & Reason Test: Triangles - Question 7
In case of assertion

In ΔPQD and ΔRPD, ∠PDQ = ∠PDR= 90°.

There is no other information to be similar.

Thus, it is not it will be correct to say that ΔPQD ~ ΔRPD.

∴ Assertion is incorrect.

In case of reason:

In ΔADE and ΔACB, we have

∠ADE= ∠ACB [Given]

∠DAE= ∠CAB [Common angle]

By AA similarity, we get ΔADE ~ ΔACB.

∴ Reason is correct

Hence, assertion is incorrect but reason is correct

Assertion & Reason Test: Triangles - Question 8
Save

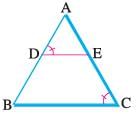
Direction: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.

Assertion : ABC is an isosceles, right triangle, right angled at C . Then AB2 = 3AC2

Reason : In an isosceles triangle ABC if AC = BC and AB2 = 2AC2 , then ∠C = 90°
Detailed Solution for Assertion & Reason Test: Triangles - Question 8
If Assertion is incorrect, but Reason is correct.

In right angled ΔABC ,

AB2 = AC2 + BC2(By Pythagoras Theorem)

= AC2 + AC2 [BC = AC]

= 2AC2AB2 = 2AC2

Assertion is false.

Again since, AB2 = 2AC2

= AC2 + AC2 = AC2 + BC2 (AC = BC given)

∠ = 90°

(By converse of Pythagoras Theorem)Reason is true.

Assertion & Reason Test: Triangles - Question 9
Save

Direction: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.

Assertion : In ∆ABC , AB = 6√3, AC = 12 cm and BC = 6cm then ∠B = 90°.

Reason : If in a triangle, square of one side is equal to the sum of the squares of the other two sides, then the angle opposite the first side is a right angle.
Detailed Solution for Assertion & Reason Test: Triangles - Question 9
We know that If in a triangle, square of one side is equal to the sum of the squares of the other two sides, then the angle opposite the first side is a right angle. This is converse of Pythagoras theorem.

So, Reason is correct

Now, AB2 = (6√3)2 = 108

AC2 = 122 = 144

and BC2 = 62 = 36

∴ 2 = 2 + 2

By converse of Pythagoras theorem, ∠B = 90°

So, Assertion is also correct.

Assertion & Reason Test: Triangles - Question 10
Save

Direction: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.

Assertion (A): If in two right triangles, one of the acute angles of one triangle is equal to an acute angle of the other triangle, then triangles will be similar.

Reason (R): If the ratio of the corresponding altitudes of two similar triangles is 3/5, then the

ratio of their areas is 6/5.
Detailed Solution for Assertion & Reason Test: Triangles - Question 10
In case of assertion: In the given two right triangles, both have equal right angles and one of the acute angles of one triangle is equal to an acute angle of the other triangle.

Thus, by AA similarity, the given two triangles are similar.

∴ Assertion is correct.

In case of reason:

We know that the ratio of the areas of two similar triangles is the square of the ratio of the corresponding altitudes of two similar triangles.

Thus, the ratio of the areas of two similar triangles is (3/5)2 = 9/25.

Information about Assertion & Reason Test: Triangles Page
In this test you can find the Exam questions for Assertion & Reason Test: Triangles solved & explained in the simplest way possible. Besides giving Questions and answers for Assertion & Reason Test: Triangles, EduRev gives you an ample number of Online tests for practice

Top Courses for Grade 10

Download as PDF

Top Courses for Grade 10

Important Questions for Assertion & Reason Test: Triangles

Find all the important questions for Assertion & Reason Test: Triangles at EduRev.Get fully prepared for Assertion & Reason Test: Triangles with EduRev's comprehensive question bank and test resources. Our platform offers a diverse range of question papers covering various topics within the Assertion & Reason Test: Triangles syllabus. Whether you need to review specific subjects or assess your overall readiness, EduRev has you covered. The questions are designed to challenge you and help you gain confidence in tackling the actual exam. Maximize your chances of success by utilizing EduRev's extensive collection of Assertion & Reason Test: Triangles resources.

Assertion & Reason Test: Triangles MCQs with Answers

Prepare for the Assertion & Reason Test: Triangles within the Grade 10 exam with comprehensive MCQs and answers at EduRev. Our platform offers a wide range of practice papers, question papers, and mock tests to familiarize you with the exam pattern and syllabus. Access the best books, study materials, and notes curated by toppers to enhance your preparation. Stay updated with the exam date and receive expert preparation tips and paper analysis. Visit EduRev's official website today and access a wealth of videos and coaching resources to excel in your exam.

Online Tests for Assertion & Reason Test: Triangles

Practice with a wide array of question papers that follow the exam pattern and syllabus. Our platform offers a user-friendly interface, allowing you to track your progress and identify areas for improvement. Access detailed solutions and explanations for each test to enhance your understanding of concepts. With EduRev's Online Tests, you can build confidence, boost your performance, and ace Assertion & Reason Test: Triangles with ease. Join thousands of successful students who have benefited from our trusted online resources.
© EduRev
Education Revolution
Signup to see your scores go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup