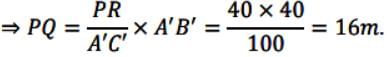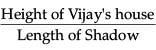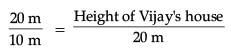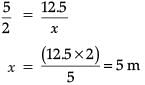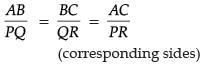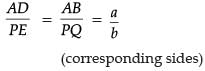Case Based Questions Test: Triangles - 2 - EmSAT Achieve MCQ
10 Questions MCQ Test - Case Based Questions Test: Triangles - 2
Direction: Read the following text and answer the below questions:
SIMILAR TRIANGLES
Vijay is trying to find the average height of a tower near his house. He is using the properties of similar triangles. The height of Vijay’s house if 20 m when Vijay’s house casts a shadow 10 m long on the ground. At the same time, the tower casts a shadow 50 m long on the ground and the house of Ajay casts 20 m shadow on the ground.
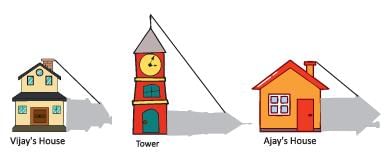
When the tower casts a shadow of 40 m, same time what will be the length of the shadow of Vijay’s house?
Direction: Read the following text and answer the below questions:
SIMILAR TRIANGLES
Vijay is trying to find the average height of a tower near his house. He is using the properties of similar triangles. The height of Vijay’s house if 20 m when Vijay’s house casts a shadow 10 m long on the ground. At the same time, the tower casts a shadow 50 m long on the ground and the house of Ajay casts 20 m shadow on the ground.
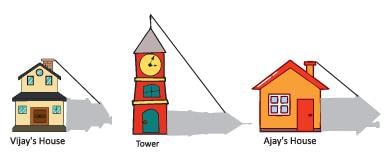
What will be the length of the shadow of the tower when Vijay’s house casts a shadow of 12 m?
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Direction: Read the following text and answer the below questions:
SIMILAR TRIANGLES
Vijay is trying to find the average height of a tower near his house. He is using the properties of similar triangles. The height of Vijay’s house if 20 m when Vijay’s house casts a shadow 10 m long on the ground. At the same time, the tower casts a shadow 50 m long on the ground and the house of Ajay casts 20 m shadow on the ground.
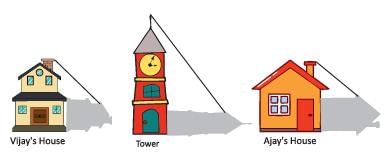
When the tower casts a shadow of 40 m, same time what will be the length of the shadow of Ajay’s house?
Direction: Read the following text and answer the below questions:
SIMILAR TRIANGLES
Vijay is trying to find the average height of a tower near his house. He is using the properties of similar triangles. The height of Vijay’s house if 20 m when Vijay’s house casts a shadow 10 m long on the ground. At the same time, the tower casts a shadow 50 m long on the ground and the house of Ajay casts 20 m shadow on the ground.
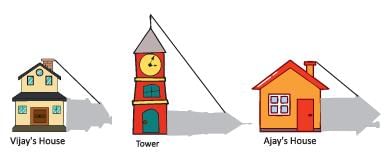
What is the height of the tower?
Direction: Read the following text and answer the below questions:
SIMILAR TRIANGLES
Vijay is trying to find the average height of a tower near his house. He is using the properties of similar triangles. The height of Vijay’s house if 20 m when Vijay’s house casts a shadow 10 m long on the ground. At the same time, the tower casts a shadow 50 m long on the ground and the house of Ajay casts 20 m shadow on the ground.
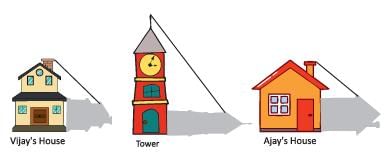
What is the height of Ajay’s house?
Direction: Read the following text and answer the following questions on the basis of the same:
SCALE FACTOR AND SIMILARITY SCALE FACTOR
A scale drawing of an object is of the same shape as the object but of a different size.
The scale of a drawing is a comparison of the length used on a drawing to the length it represents. The value of scale is written as a ratio.
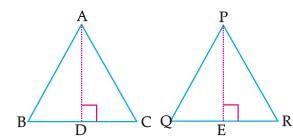
SIMILAR FIGURES
The ratio of two corresponding sides in similar figures is called the scale factor.
If one shape can become another using Resizing then the shapes are Similar.
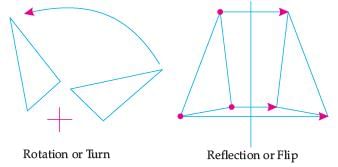
Hence, two shapes are Similar when one can become the other after a resize, flip, slide or turn.
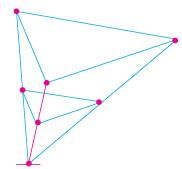
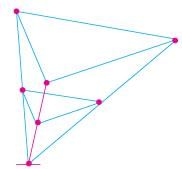
Below you see a student's mathematical model of a farmhouse roof with measurements. The attic floor, ABCD in the model, is a square. The beams that support the roof are the edge of a rectangular prism, EFGHKLMN.
E is the middle of AT, F is the middle of BT, G is the middle of CT, and H is the middle of DT. All the edges of the pyramid in the model have length of 12 m.
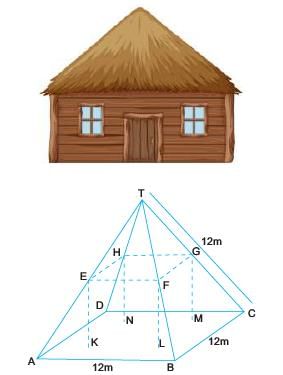
What is the length of EF, where EF is one of the horizontal edges of the block ?
Direction: Read the following text and answer the following questions on the basis of the same:
SCALE FACTOR AND SIMILARITY SCALE FACTOR
A scale drawing of an object is of the same shape as the object but of a different size.
The scale of a drawing is a comparison of the length used on a drawing to the length it represents. The value of scale is written as a ratio.
SIMILAR FIGURES
The ratio of two corresponding sides in similar figures is called the scale factor.
If one shape can become another using Resizing then the shapes are Similar.
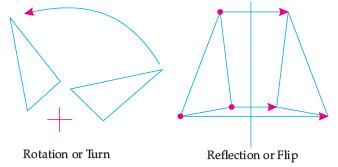
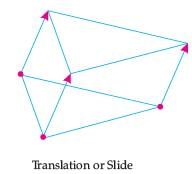
Hence, two shapes are Similar when one can become the other after a resize, flip, slide or turn.
What will effect the similarity of any two polygons ?
Direction: Read the following text and answer the following questions on the basis of the same:
SCALE FACTOR AND SIMILARITY SCALE FACTOR
A scale drawing of an object is of the same shape as the object but of a different size.
The scale of a drawing is a comparison of the length used on a drawing to the length it represents. The value of scale is written as a ratio.
SIMILAR FIGURES
The ratio of two corresponding sides in similar figures is called the scale factor.
If one shape can become another using Resizing then the shapes are Similar.
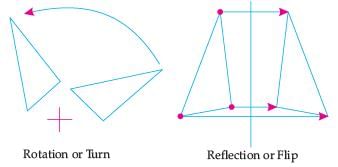
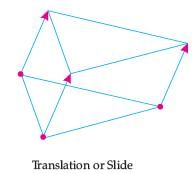
Hence, two shapes are Similar when one can become the other after a resize, flip, slide or turn.
The shadow of a stick 5 m long is 2 m. At the same time the shadow of a tree 12.5 m high is
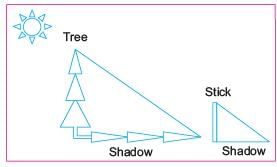
Direction: Read the following text and answer the following questions on the basis of the same:
SCALE FACTOR AND SIMILARITY SCALE FACTOR
A scale drawing of an object is of the same shape as the object but of a different size.
The scale of a drawing is a comparison of the length used on a drawing to the length it represents. The value of scale is written as a ratio.
SIMILAR FIGURES
The ratio of two corresponding sides in similar figures is called the scale factor.
If one shape can become another using Resizing then the shapes are Similar.
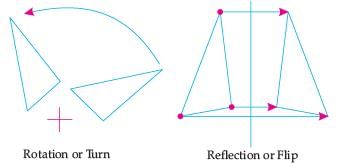
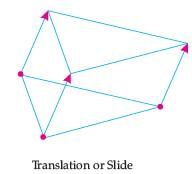
Hence, two shapes are Similar when one can become the other after a resize, flip, slide or turn.
A model of a boat is made on the scale of 1 : 4. The model is 120 cm long. The full size of the boat has a width of 60 cm. What is the width of the scale model ?
Direction: Read the following text and answer the following questions on the basis of the same:
SCALE FACTOR AND SIMILARITY SCALE FACTOR
A scale drawing of an object is of the same shape as the object but of a different size.
The scale of a drawing is a comparison of the length used on a drawing to the length it represents. The value of scale is written as a ratio.
SIMILAR FIGURES
The ratio of two corresponding sides in similar figures is called the scale factor.
If one shape can become another using Resizing then the shapes are Similar.
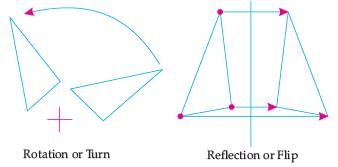
Hence, two shapes are Similar when one can become the other after a resize, flip, slide or turn.
If two similar triangles have a scale factor of a : b, which statement regarding the two triangles is true ?
Top Courses for EmSAT Achieve
Important Questions for Case Based Questions Test: Triangles - 2
Case Based Questions Test: Triangles - 2 MCQs with Answers
Online Tests for Case Based Questions Test: Triangles - 2
|
© EduRev
|
Education Revolution
|
|
