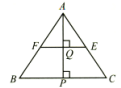All Courses
Get the App Signup / Login
Sign in Open App
Class 9 Exam  >  Class 9 Tests  >  Test: Quadrilaterals- Assertion & Reason Type Questions - Class 9 MCQ

Test: Quadrilaterals- Assertion & Reason Type Questions - Class 9 MCQ


Test Description

10 Questions MCQ Test - Test: Quadrilaterals- Assertion & Reason Type Questions

Test: Quadrilaterals- Assertion & Reason Type Questions for Class 9 2024 is part of Class 9 preparation. The Test: Quadrilaterals- Assertion & Reason Type Questions questions and answers have been prepared according to the Class 9 exam syllabus.The Test: Quadrilaterals- Assertion & Reason Type Questions MCQs are made for Class 9 2024 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests for Test: Quadrilaterals- Assertion & Reason Type Questions below.
Solutions of Test: Quadrilaterals- Assertion & Reason Type Questions questions in English are available as part of our course for Class 9 & Test: Quadrilaterals- Assertion & Reason Type Questions solutions in Hindi for Class 9 course. Download more important topics, notes, lectures and mock test series for Class 9 Exam by signing up for free. Attempt Test: Quadrilaterals- Assertion & Reason Type Questions | 10 questions in 20 minutes | Mock test for Class 9 preparation | Free important questions MCQ to study for Class 9 Exam | Download free PDF with solutions
Test: Quadrilaterals- Assertion & Reason Type Questions - Question 1
Save

Direction: In each of the following questions, a statement of Assertion is given followed by a corresponding statement of Reason just below it. Of the statements, mark the correct.

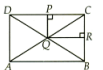
Assertion : ABCD and PQRC are rectangles and Q is a midpoint of AC . Then DP = PC.

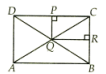
Reason : The line segment joining the midpoint of any two sides of a triangle is parallel to the third side and equal to half of it.

Detailed Solution for Test: Quadrilaterals- Assertion & Reason Type Questions - Question 1

The correct option is B If both assertion and reason are true but reason is not the correct explanation of assertion
In ΔADC, Q is the mid-point of AC such that PQ∥AD
∴ P is the mid-point of DC
⇒ DP = PC [using converse of mid-point theorem]


∴ Assertion is true, reason is true but reason is not correct explanation of assertion.

Test: Quadrilaterals- Assertion & Reason Type Questions - Question 2
Save

Direction: In each of the following questions, a statement of Assertion is given followed by a corresponding statement of Reason just below it. Of the statements, mark the correct.

Assertion : Two opposite angles of a parallelogram are (3x - 2º) and (50 - x)º . The measure of one of the angle is 37º.

Reason : Opposite angles of a parallelogram are equal.

Detailed Solution for Test: Quadrilaterals- Assertion & Reason Type Questions - Question 2
Since, opposite angles of a parallelogram are equal.

Therefore, 3x - 2 = 50 - x

x = 13

One angle is 37º

1 Crore+ students have signed up on EduRev. Have you? Download the App
Test: Quadrilaterals- Assertion & Reason Type Questions - Question 3
Save

Direction: In each of the following questions, a statement of Assertion is given followed by a corresponding statement of Reason just below it. Of the statements, mark the correct.

Assertion : In ΔABC , E and F are the midpoints of AC and AB respectively. The altitude AP at BC intersects FE at Q. Then, AQ QP = .

Reason : Q is the midpoint of AP.

Detailed Solution for Test: Quadrilaterals- Assertion & Reason Type Questions - Question 3
In ΔABC , E and F are midpoint of the sides AC

and AB respectively.

FE || BC [By mid-point theorem]

Now, in ΔABP, F is mid-point of AB and FQ || BP.

Q is mid-point of AP

AQ = QP.

Test: Quadrilaterals- Assertion & Reason Type Questions - Question 4
Save

Direction: In each of the following questions, a statement of Assertion is given followed by a corresponding statement of Reason just below it. Of the statements, mark the correct.

Assertion : The angles of a quadrilateral are xº, (x - 10)º , (x + 30)º and (2x)º , the smallest angle is equal to 58º.

Reason : Sum of the angles of a quadrilateral is 360º.
Detailed Solution for Test: Quadrilaterals- Assertion & Reason Type Questions - Question 4
Given angles(in degrees) = x, x - 10, x = 30, 2x

sum of all angles 0 a quadrilateral is 360

=> x + x - 10 + x + 30 + 2x = 360

=> 5x = 20 = 360

=> 5x = 340

=> x = 68

smallest angle is x - 10

i.e. 68 - 10 = 58 degrees.

Test: Quadrilaterals- Assertion & Reason Type Questions - Question 5
Save

Direction: In each of the following questions, a statement of Assertion is given followed by a corresponding statement of Reason just below it. Of the statements, mark the correct.

Assertion : A parallelogram consists of two congruent triangles.

Reason : Diagonal of a parallelogram divides it into two congruent triangles.
Detailed Solution for Test: Quadrilaterals- Assertion & Reason Type Questions - Question 5

In ΔBAC and ΔDCA

∠1 = ∠2

∠3 = ∠4 [alternate pair]

AC = AC (common)

ΔBAC ≅ ΔDCA (By ASA)

Therefore, diagonal of a parallelogram divides it into two congruent triangles.

Test: Quadrilaterals- Assertion & Reason Type Questions - Question 6
Save

Direction: In each of the following questions, a statement of Assertion is given followed by a corresponding statement of Reason just below it. Of the statements, mark the correct.

Assertion : If the diagonals of a parallelogram ABCD are equal, then ∠ABC = 90º.

Reason : If the diagonals of a parallelogram are equal, it becomes a rectangle.
Detailed Solution for Test: Quadrilaterals- Assertion & Reason Type Questions - Question 6

Let ABCD be a parallelogram. To show that ABCD is a rectangle, we have to prove that one of its interior angles is 90º.

In ΔABC and ΔDCB,

AB = DC (Opposite sides of a parallelogram are equal)

BC = BC (Common)

AC = DB (Given)

∴ ΔABC ≅ ΔDCB (By SSS Congruence rule)

⇒ ∠ABC = ∠DCB

It is known that the sum of the measures of angles on the same side of transversal is 180º.

∠ABC + ∠DCB = 180º (AB || CD)

⇒ ∠ABC + ∠ABC = 180º

⇒ 2∠ABC = 180º

⇒ ∠ABC = 90º

Since ABCD is a parallelogram and one of its interior angles is 90º, ABCD is a rectangle.

Test: Quadrilaterals- Assertion & Reason Type Questions - Question 7
Save

Direction: In each of the following questions, a statement of Assertion is given followed by a corresponding statement of Reason just below it. Of the statements, mark the correct.

Assertion : If the angles of a quadrilateral are in the ratio 2 : 3 : 7 : 6, then the measure of angles are 40º, 60º, 140º, 120º, respectively.

Reason : The sum of the angles of a quadrilateral is 360º.
Detailed Solution for Test: Quadrilaterals- Assertion & Reason Type Questions - Question 7
2x + 3x + 7x + 6x = 360º

=> 18x = 360º

=> x = 360º/18 = 20º

First angle = 2 × 20º = 40º

Second angle = 3 × 20º = 60º

Third angle = 7 x 20º = 140º

Fourth angle = 6 x 20º = 120º

Test: Quadrilaterals- Assertion & Reason Type Questions - Question 8
Save

Direction: In each of the following questions, a statement of Assertion is given followed by a corresponding statement of Reason just below it. Of the statements, mark the correct.

Assertion : ABCD is a square. AC and BD intersect at O. The measure of ∠AOB = 90º.

Reason : Diagonals of a square bisect each other at right angles.
Detailed Solution for Test: Quadrilaterals- Assertion & Reason Type Questions - Question 8
Since, diagonals of a square bisect each other at right angles.

∠AOB = 90º

Test: Quadrilaterals- Assertion & Reason Type Questions - Question 9
Save

Direction: In each of the following questions, a statement of Assertion is given followed by a corresponding statement of Reason just below it. Of the statements, mark the correct.

Assertion : In ΔABC , median AD is produced to X such that AD DX = . Then ABXC is a parallelogram.

Reason : Diagonals AX and BC bisect each other at right angles.
Detailed Solution for Test: Quadrilaterals- Assertion & Reason Type Questions - Question 9
In quadrilateral ABXC , we have

AD = DX [Given]

BD = DC [Given]

So, diagonals AX and BC bisect each other but not

at right angles.

Therefore, ABXC is a parallelogram

Test: Quadrilaterals- Assertion & Reason Type Questions - Question 10
Save

Direction: In each of the following questions, a statement of Assertion is given followed by a corresponding statement of Reason just below it. Of the statements, mark the correct.

Assertion : The consecutive sides of a quadrilateral have one common point.

Reason : The opposite sides of a quadrilateral have two common point.
Detailed Solution for Test: Quadrilaterals- Assertion & Reason Type Questions - Question 10

Two sides of a quadrilateral are called its opposite sides if they do not have a common end point.

In the given figure, (AB, DC) and (AD, BC) are two pairs of opposite sides of quadrilateral ABCD.

Two angles of a quadrilateral having a common arm are called its adjacent angles.

Information about Test: Quadrilaterals- Assertion & Reason Type Questions Page
In this test you can find the Exam questions for Test: Quadrilaterals- Assertion & Reason Type Questions solved & explained in the simplest way possible. Besides giving Questions and answers for Test: Quadrilaterals- Assertion & Reason Type Questions, EduRev gives you an ample number of Online tests for practice

Top Courses for Class 9

Download as PDF

Top Courses for Class 9

Important Questions for Quadrilaterals- Assertion & Reason Type Questions

Find all the important questions for Quadrilaterals- Assertion & Reason Type Questions at EduRev.Get fully prepared for Quadrilaterals- Assertion & Reason Type Questions with EduRev's comprehensive question bank and test resources. Our platform offers a diverse range of question papers covering various topics within the Quadrilaterals- Assertion & Reason Type Questions syllabus. Whether you need to review specific subjects or assess your overall readiness, EduRev has you covered. The questions are designed to challenge you and help you gain confidence in tackling the actual exam. Maximize your chances of success by utilizing EduRev's extensive collection of Quadrilaterals- Assertion & Reason Type Questions resources.

Quadrilaterals- Assertion & Reason Type Questions MCQs with Answers

Prepare for the Quadrilaterals- Assertion & Reason Type Questions within the Class 9 exam with comprehensive MCQs and answers at EduRev. Our platform offers a wide range of practice papers, question papers, and mock tests to familiarize you with the exam pattern and syllabus. Access the best books, study materials, and notes curated by toppers to enhance your preparation. Stay updated with the exam date and receive expert preparation tips and paper analysis. Visit EduRev's official website today and access a wealth of videos and coaching resources to excel in your exam.

Online Tests for Quadrilaterals- Assertion & Reason Type Questions

Practice with a wide array of question papers that follow the exam pattern and syllabus. Our platform offers a user-friendly interface, allowing you to track your progress and identify areas for improvement. Access detailed solutions and explanations for each test to enhance your understanding of concepts. With EduRev's Online Tests, you can build confidence, boost your performance, and ace Quadrilaterals- Assertion & Reason Type Questions with ease. Join thousands of successful students who have benefited from our trusted online resources.
© EduRev
Education Revolution
Signup to see your scores go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup