Case Based Questions Test: Kinetic Theory - Grade 11 MCQ
10 Questions MCQ Test - Case Based Questions Test: Kinetic Theory
Attempt All sub parts from each question.
Atomic Hypothesis in Ancient India and Greece Though John Dalton is credited with the introduction of atomic view point in modern science, scholars in ancient India and Greece conjectured long before the existence of atoms and molecules. In the Vaisheshika school of thought in India founded by Kanada (Sixth century B.C.) the atomic picture was developed in considerable detail. Atoms were thought to be eternal, indivisible, infinitesimal and ultimate parts of matter. It was argued that if matter could be subdivided without an end, there would be no difference between a mustard seed and the Meru mountain. The four kinds of atoms (Paramanu — Sanskrit word for the smallest particle) postulated were Bhoomi (Earth), Ap (water), Tejas (fire) and Vayu (air) that have characteristic mass and other attributes, we re propounded. Akasa (space) was thought to have no atomic structure and was continuous and inert. Atoms combine to form different molecules (e.g. two atoms combine to form a diatomic molecule dvyanuka, three atoms form a tryanuka or a triatomic molecule), their properties depending upon the nature and ratio of the constituent atoms. The size of the atoms was also estimated, by conjecture or by methods that are not known to us. The estimates vary. In Lalitavistara, a famous biography of the Buddha written mainly in the second century B.C., the estimate is close to the modern estimate of atomic size, of the order of 10–10 m. In ancient Greece, Democritus (Fourth century B.C.) is best known for his atomic hypothesis. The word ‘atom’ means ‘indivisible’ in Greek. According to him, atoms differ from each other physically, in shape, size and other properties and this resulted in the different properties of the substances formed by their combination. The atoms of water were smooth and round and unable to ‘hook’ on to each other, which is why liquid /water flows easily. The atoms of earth were rough and jagged, so they held together to form hard substances. The atoms of fire were thorny which is why it caused painful burns. These fascinating ideas, despite their ingenuity, could not evolve much further, perhaps because they were intuitive conjectures and speculations not tested and modified by quantitative experiments–the hallmark of modern science.
Q. In Greek, “atom” means
Attempt All sub parts from each question.
Atomic Hypothesis in Ancient India and Greece Though John Dalton is credited with the introduction of atomic view point in modern science, scholars in ancient India and Greece conjectured long before the existence of atoms and molecules. In the Vaisheshika school of thought in India founded by Kanada (Sixth century B.C.) the atomic picture was developed in considerable detail. Atoms were thought to be eternal, indivisible, infinitesimal and ultimate parts of matter. It was argued that if matter could be subdivided without an end, there would be no difference between a mustard seed and the Meru mountain. The four kinds of atoms (Paramanu — Sanskrit word for the smallest particle) postulated were Bhoomi (Earth), Ap (water), Tejas (fire) and Vayu (air) that have characteristic mass and other attributes, we re propounded. Akasa (space) was thought to have no atomic structure and was continuous and inert. Atoms combine to form different molecules (e.g. two atoms combine to form a diatomic molecule dvyanuka, three atoms form a tryanuka or a triatomic molecule), their properties depending upon the nature and ratio of the constituent atoms. The size of the atoms was also estimated, by conjecture or by methods that are not known to us. The estimates vary. In Lalitavistara, a famous biography of the Buddha written mainly in the second century B.C., the estimate is close to the modern estimate of atomic size, of the order of 10–10 m. In ancient Greece, Democritus (Fourth century B.C.) is best known for his atomic hypothesis. The word ‘atom’ means ‘indivisible’ in Greek. According to him, atoms differ from each other physically, in shape, size and other properties and this resulted in the different properties of the substances formed by their combination. The atoms of water were smooth and round and unable to ‘hook’ on to each other, which is why liquid /water flows easily. The atoms of earth were rough and jagged, so they held together to form hard substances. The atoms of fire were thorny which is why it caused painful burns. These fascinating ideas, despite their ingenuity, could not evolve much further, perhaps because they were intuitive conjectures and speculations not tested and modified by quantitative experiments–the hallmark of modern science.
Q. The kinds of atoms which were propounded in ancient India are
Attempt All sub parts from each question.
Atomic Hypothesis in Ancient India and Greece Though John Dalton is credited with the introduction of atomic view point in modern science, scholars in ancient India and Greece conjectured long before the existence of atoms and molecules. In the Vaisheshika school of thought in India founded by Kanada (Sixth century B.C.) the atomic picture was developed in considerable detail. Atoms were thought to be eternal, indivisible, infinitesimal and ultimate parts of matter. It was argued that if matter could be subdivided without an end, there would be no difference between a mustard seed and the Meru mountain. The four kinds of atoms (Paramanu — Sanskrit word for the smallest particle) postulated were Bhoomi (Earth), Ap (water), Tejas (fire) and Vayu (air) that have characteristic mass and other attributes, we re propounded. Akasa (space) was thought to have no atomic structure and was continuous and inert. Atoms combine to form different molecules (e.g. two atoms combine to form a diatomic molecule dvyanuka, three atoms form a tryanuka or a triatomic molecule), their properties depending upon the nature and ratio of the constituent atoms. The size of the atoms was also estimated, by conjecture or by methods that are not known to us. The estimates vary. In Lalitavistara, a famous biography of the Buddha written mainly in the second century B.C., the estimate is close to the modern estimate of atomic size, of the order of 10–10 m. In ancient Greece, Democritus (Fourth century B.C.) is best known for his atomic hypothesis. The word ‘atom’ means ‘indivisible’ in Greek. According to him, atoms differ from each other physically, in shape, size and other properties and this resulted in the different properties of the substances formed by their combination. The atoms of water were smooth and round and unable to ‘hook’ on to each other, which is why liquid /water flows easily. The atoms of earth were rough and jagged, so they held together to form hard substances. The atoms of fire were thorny which is why it caused painful burns. These fascinating ideas, despite their ingenuity, could not evolve much further, perhaps because they were intuitive conjectures and speculations not tested and modified by quantitative experiments–the hallmark of modern science.
Q. In ancient Greece, who is best known for his atomic hypothesis?
Attempt All sub parts from each question.
Atomic Hypothesis in Ancient India and Greece Though John Dalton is credited with the introduction of atomic view point in modern science, scholars in ancient India and Greece conjectured long before the existence of atoms and molecules. In the Vaisheshika school of thought in India founded by Kanada (Sixth century B.C.) the atomic picture was developed in considerable detail. Atoms were thought to be eternal, indivisible, infinitesimal and ultimate parts of matter. It was argued that if matter could be subdivided without an end, there would be no difference between a mustard seed and the Meru mountain. The four kinds of atoms (Paramanu — Sanskrit word for the smallest particle) postulated were Bhoomi (Earth), Ap (water), Tejas (fire) and Vayu (air) that have characteristic mass and other attributes, we re propounded. Akasa (space) was thought to have no atomic structure and was continuous and inert. Atoms combine to form different molecules (e.g. two atoms combine to form a diatomic molecule dvyanuka, three atoms form a tryanuka or a triatomic molecule), their properties depending upon the nature and ratio of the constituent atoms. The size of the atoms was also estimated, by conjecture or by methods that are not known to us. The estimates vary. In Lalitavistara, a famous biography of the Buddha written mainly in the second century B.C., the estimate is close to the modern estimate of atomic size, of the order of 10–10 m. In ancient Greece, Democritus (Fourth century B.C.) is best known for his atomic hypothesis. The word ‘atom’ means ‘indivisible’ in Greek. According to him, atoms differ from each other physically, in shape, size and other properties and this resulted in the different properties of the substances formed by their combination. The atoms of water were smooth and round and unable to ‘hook’ on to each other, which is why liquid /water flows easily. The atoms of earth were rough and jagged, so they held together to form hard substances. The atoms of fire were thorny which is why it caused painful burns. These fascinating ideas, despite their ingenuity, could not evolve much further, perhaps because they were intuitive conjectures and speculations not tested and modified by quantitative experiments–the hallmark of modern science.
Q. Which of the followings was thought to have no atomic structure and was continuous and inert?
Attempt All sub parts from each question.
Atomic Hypothesis in Ancient India and Greece Though John Dalton is credited with the introduction of atomic view point in modern science, scholars in ancient India and Greece conjectured long before the existence of atoms and molecules. In the Vaisheshika school of thought in India founded by Kanada (Sixth century B.C.) the atomic picture was developed in considerable detail. Atoms were thought to be eternal, indivisible, infinitesimal and ultimate parts of matter. It was argued that if matter could be subdivided without an end, there would be no difference between a mustard seed and the Meru mountain. The four kinds of atoms (Paramanu — Sanskrit word for the smallest particle) postulated were Bhoomi (Earth), Ap (water), Tejas (fire) and Vayu (air) that have characteristic mass and other attributes, we re propounded. Akasa (space) was thought to have no atomic structure and was continuous and inert. Atoms combine to form different molecules (e.g. two atoms combine to form a diatomic molecule dvyanuka, three atoms form a tryanuka or a triatomic molecule), their properties depending upon the nature and ratio of the constituent atoms. The size of the atoms was also estimated, by conjecture or by methods that are not known to us. The estimates vary. In Lalitavistara, a famous biography of the Buddha written mainly in the second century B.C., the estimate is close to the modern estimate of atomic size, of the order of 10–10 m. In ancient Greece, Democritus (Fourth century B.C.) is best known for his atomic hypothesis. The word ‘atom’ means ‘indivisible’ in Greek. According to him, atoms differ from each other physically, in shape, size and other properties and this resulted in the different properties of the substances formed by their combination. The atoms of water were smooth and round and unable to ‘hook’ on to each other, which is why liquid /water flows easily. The atoms of earth were rough and jagged, so they held together to form hard substances. The atoms of fire were thorny which is why it caused painful burns. These fascinating ideas, despite their ingenuity, could not evolve much further, perhaps because they were intuitive conjectures and speculations not tested and modified by quantitative experiments–the hallmark of modern science.
Q. In which biography the size of the atoms was estimated close to the modern estimate
Maxwell Distribution Function In a given mass of gas, the velocities of all molecules are not the same, even when bulk parameters like pressure, volume and temperature are fixed. Collisions change the direction and the speed of molecules. However in a state of equilibrium, the distribution of speeds is constant or fixed. Distributions are very important and useful when dealing with systems containing large number of objects. As an example consider the ages of different persons in a city. It is not feasible to deal with the age of each individual. We can divide the people into groups: children up to age 20 years, adults between ages of 20 and 60, old people above 60. If we want more detailed information we can choose smaller intervals, 0–1, 1–2,..., 99– 100 of age groups. When the size of the interval becomes smaller, say half year, the number of persons in the interval will also reduce, roughly half the original number in the one year interval. The number of persons dN(x) in the age interval x and x + dx is proportional to dx or dN(x) = nx dx. We have used nx to denote the number of persons at the value of x. In a similar way the molecular speed distribution gives the number of molecules between the speeds v and v + dv. dN(v) = 4p N a3 e–bv2v2dv = nvdv. This is called Maxwell distribution.
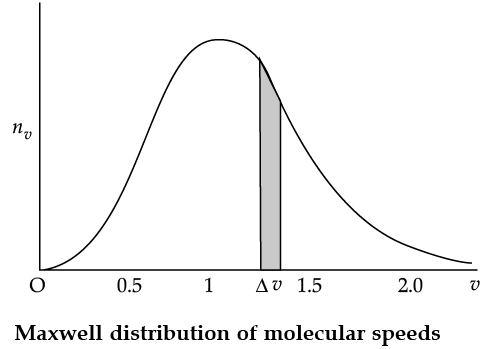
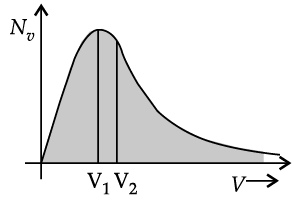
The plot of nv against v is shown in the figure. The fraction of the molecules with speeds v and v + dv is equal to the area of the strip shown. The average of any quantity like v2 is defined by the integral
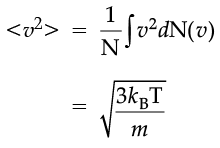
which agrees with the result derived from more elementary considerations.
Q. When pressure, volume and temperature are fixed, in a given mass of gas, the velocities of all molecules
Maxwell Distribution Function In a given mass of gas, the velocities of all molecules are not the same, even when bulk parameters like pressure, volume and temperature are fixed. Collisions change the direction and the speed of molecules. However in a state of equilibrium, the distribution of speeds is constant or fixed. Distributions are very important and useful when dealing with systems containing large number of objects. As an example consider the ages of different persons in a city. It is not feasible to deal with the age of each individual. We can divide the people into groups: children up to age 20 years, adults between ages of 20 and 60, old people above 60. If we want more detailed information we can choose smaller intervals, 0–1, 1–2,..., 99– 100 of age groups. When the size of the interval becomes smaller, say half year, the number of persons in the interval will also reduce, roughly half the original number in the one year interval. The number of persons dN(x) in the age interval x and x + dx is proportional to dx or dN(x) = nx dx. We have used nx to denote the number of persons at the value of x. In a similar way the molecular speed distribution gives the number of molecules between the speeds v and v + dv. dN(v) = 4p N a3 e–bv2v2dv = nvdv. This is called Maxwell distribution.
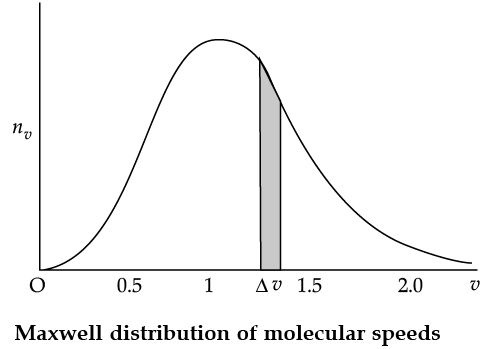
The plot of nv against v is shown in the figure. The fraction of the molecules with speeds v and v + dv is equal to the area of the strip shown. The average of any quantity like v2 is defined by the integral
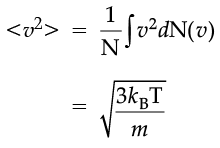
which agrees with the result derived from more elementary considerations.
Q. The molecular speed distribution of number of molecules between the speeds v and v+ dv is given by
Maxwell Distribution Function In a given mass of gas, the velocities of all molecules are not the same, even when bulk parameters like pressure, volume and temperature are fixed. Collisions change the direction and the speed of molecules. However in a state of equilibrium, the distribution of speeds is constant or fixed. Distributions are very important and useful when dealing with systems containing large number of objects. As an example consider the ages of different persons in a city. It is not feasible to deal with the age of each individual. We can divide the people into groups: children up to age 20 years, adults between ages of 20 and 60, old people above 60. If we want more detailed information we can choose smaller intervals, 0–1, 1–2,..., 99– 100 of age groups. When the size of the interval becomes smaller, say half year, the number of persons in the interval will also reduce, roughly half the original number in the one year interval. The number of persons dN(x) in the age interval x and x + dx is proportional to dx or dN(x) = nx dx. We have used nx to denote the number of persons at the value of x. In a similar way the molecular speed distribution gives the number of molecules between the speeds v and v + dv. dN(v) = 4p N a3 e–bv2v2dv = nvdv. This is called Maxwell distribution.
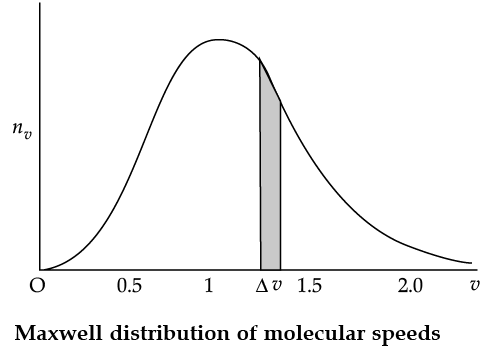
The plot of nv against v is shown in the figure. The fraction of the molecules with speeds v and v + dv is equal to the area of the strip shown. The average of any quantity like v2 is defined by the integral
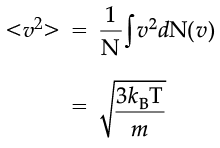
which agrees with the result derived from more elementary considerations.
Q. From the given graph determine the number of molecules at zero speed.
Maxwell Distribution Function In a given mass of gas, the velocities of all molecules are not the same, even when bulk parameters like pressure, volume and temperature are fixed. Collisions change the direction and the speed of molecules. However in a state of equilibrium, the distribution of speeds is constant or fixed. Distributions are very important and useful when dealing with systems containing large number of objects. As an example consider the ages of different persons in a city. It is not feasible to deal with the age of each individual. We can divide the people into groups: children up to age 20 years, adults between ages of 20 and 60, old people above 60. If we want more detailed information we can choose smaller intervals, 0–1, 1–2,..., 99– 100 of age groups. When the size of the interval becomes smaller, say half year, the number of persons in the interval will also reduce, roughly half the original number in the one year interval. The number of persons dN(x) in the age interval x and x + dx is proportional to dx or dN(x) = nx dx. We have used nx to denote the number of persons at the value of x. In a similar way the molecular speed distribution gives the number of molecules between the speeds v and v + dv. dN(v) = 4p N a3 e–bv2v2dv = nvdv. This is called Maxwell distribution.
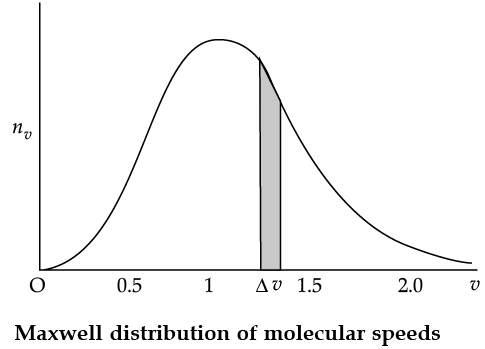
The plot of nv against v is shown in the figure. The fraction of the molecules with speeds v and v + dv is equal to the area of the strip shown. The average of any quantity like v2 is defined by the integral
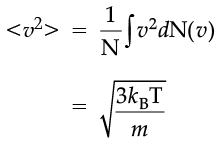
which agrees with the result derived from more elementary considerations.
Q. For a given mass of gas, in a state of equilibrium, the distribution of speeds
Maxwell Distribution Function In a given mass of gas, the velocities of all molecules are not the same, even when bulk parameters like pressure, volume and temperature are fixed. Collisions change the direction and the speed of molecules. However in a state of equilibrium, the distribution of speeds is constant or fixed. Distributions are very important and useful when dealing with systems containing large number of objects. As an example consider the ages of different persons in a city. It is not feasible to deal with the age of each individual. We can divide the people into groups: children up to age 20 years, adults between ages of 20 and 60, old people above 60. If we want more detailed information we can choose smaller intervals, 0–1, 1–2,..., 99– 100 of age groups. When the size of the interval becomes smaller, say half year, the number of persons in the interval will also reduce, roughly half the original number in the one year interval. The number of persons dN(x) in the age interval x and x + dx is proportional to dx or dN(x) = nx dx. We have used nx to denote the number of persons at the value of x. In a similar way the molecular speed distribution gives the number of molecules between the speeds v and v + dv. dN(v) = 4p N a3 e–bv2v2dv = nvdv. This is called Maxwell distribution.
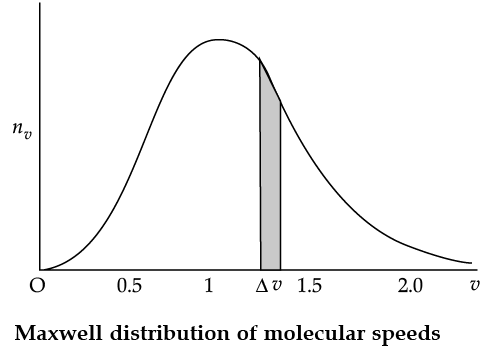
The plot of nv against v is shown in the figure. The fraction of the molecules with speeds v and v + dv is equal to the area of the strip shown. The average of any quantity like v2 is defined by the integral
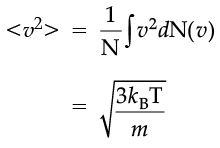
which agrees with the result derived from more elementary considerations.
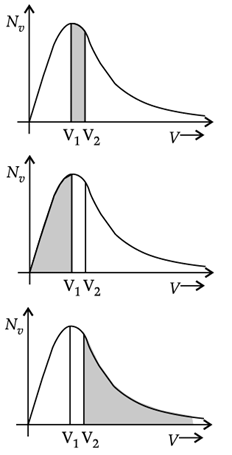
Q. The plots of nv against V are shown in the figures. Which figure shows the fraction of the molecules with speeds between V1 and V2 shown by shaded area?