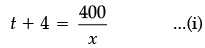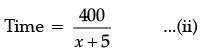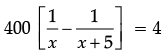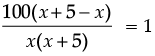Quadratic Equations - Free Case Based Type Questions with solutions
MCQ Practice Test & Solutions: Case Based Questions Test: Quadratic Equations (15 Questions)
You can prepare effectively for Class 10 Mathematics (Maths) Class 10 with this dedicated MCQ Practice Test (available with solutions) on the important topic of "Case Based Questions Test: Quadratic Equations". These 15 questions have been designed by the experts with the latest curriculum of Class 10 2026, to help you master the concept.
Test Highlights:
- - Format: Multiple Choice Questions (MCQ)
- - Duration: 30 minutes
- - Number of Questions: 15
Sign up on EduRev for free to attempt this test and track your preparation progress.
Read the following text and answer the following questions on the basis of the same:
Nidhi and Ria are very close friends. Nidhi’s parents own a Maruti Alto and Ria’s parents own a Toyota Liva. Both the families decided to go for picnic to Somnath temple in Gujarat by their own cars. Nidhi car travels x km/h when Ria’s car travels 5 km/h more than Nidhi’s car Nidhi’s car took 4 hours more than Ria’s car in covering 400 km.
Q. Which of the following quadratic equations describe the speed of Nidhi’s car?
Detailed Solution: Question 1
Read the following text and answer the following questions on the basis of the same:
Nidhi and Ria are very close friends. Nidhi’s parents own a Maruti Alto and Ria’s parents own a Toyota Liva. Both the families decided to go for picnic to Somnath temple in Gujarat by their own cars. Nidhi car travels x km/h when Ria’s car travels 5 km/h more than Nidhi’s car Nidhi’s car took 4 hours more than Ria’s car in covering 400 km.
Q. How much time took Ria to travel 400 km?
Detailed Solution: Question 2
Read the following text and answer the following questions on the basis of the same:
Nidhi and Ria are very close friends. Nidhi’s parents own a Maruti Alto and Ria’s parents own a Toyota Liva. Both the families decided to go for picnic to Somnath temple in Gujarat by their own cars. Nidhi car travels x km/h when Ria’s car travels 5 km/h more than Nidhi’s car Nidhi’s car took 4 hours more than Ria’s car in covering 400 km.
Q. What will be the distance covered by Ria’s car in two hours?
Detailed Solution: Question 3
Read the following text and answer the following questions on the basis of the same:
Nidhi and Ria are very close friends. Nidhi’s parents own a Maruti Alto and Ria’s parents own a Toyota Liva. Both the families decided to go for picnic to Somnath temple in Gujarat by their own cars. Nidhi car travels x km/h when Ria’s car travels 5 km/h more than Nidhi’s car Nidhi’s car took 4 hours more than Ria’s car in covering 400 km.
Q. What is the speed of Nidhi’s car?
Detailed Solution: Question 4
Read the following text and answer the following questions on the basis of the same:
Nidhi and Ria are very close friends. Nidhi’s parents own a Maruti Alto and Ria’s parents own a Toyota Liva. Both the families decided to go for picnic to Somnath temple in Gujarat by their own cars. Nidhi car travels x km/h when Ria’s car travels 5 km/h more than Nidhi’s car Nidhi’s car took 4 hours more than Ria’s car in covering 400 km.
Q. Name the shape of quadratic equation in graph
Detailed Solution: Question 5
Read the following text and answer the following questions on the basis of the same:
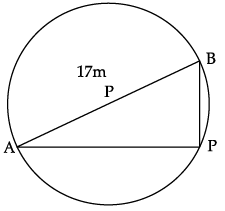
Aniket is studying in 10th standard. He created a pole on the boundary of a circular park of diameter 17 m in such a way that the difference of its distances from two diametrically opposite fixed gates A and B on the boundary is 7 m.
Q. Find the distance between pole and gate B.
Detailed Solution: Question 6
Read the following text and answer the following questions on the basis of the same:
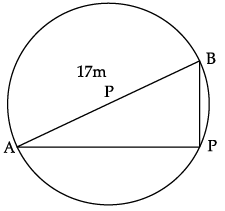
Aniket is studying in X standard. He is created a pole at on the boundary of a circular park of diameter 17 m in such a way that the difference of its distances from two diametrically opposite fixed gates A and B on the boundary is 7m.
Q. What is the length of (AP + BP)?
Detailed Solution: Question 7
Read the following text and answer the following questions on the basis of the same:
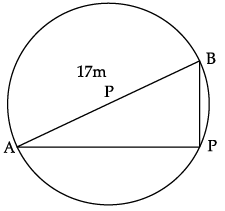
Aniket is studying in X standard. He is created a pole at on the boundary of a circular park of diameter 17 m in such a way that the difference of its distances from two diametrically opposite fixed gates A and B on the boundary is 7m.
Q. Find a quadratic equations in variable x for above situation.
Detailed Solution: Question 8
Read the following text and answer the following questions on the basis of the same:
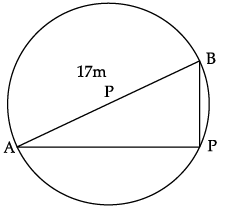
Aniket is studying in X standard. He is created a pole at on the boundary of a circular park of diameter 17 m in such a way that the difference of its distances from two diametrically opposite fixed gates A and B on the boundary is 7m.
Q. Find the distance between pole and gate A.
Detailed Solution: Question 9
Read the following text and answer the following questions on the basis of the same:
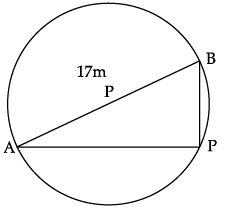
Aniket is studying in X standard. He is created a pole at on the boundary of a circular park of diameter 17 m in such a way that the difference of its distances from two diametrically opposite fixed gates A and B on the boundary is 7m.
Q. Find the area of triangle ABP.
Detailed Solution: Question 10
Read the following text and answer the following questions on the basis of the same:
A small scale industry produces a certain boxes of candles in a day. Number of boxes prepared by each worked on a particular day was 2 more than thrice the number of workers working in the industry. The number of boxes produced in a particular day was 85.
Q. Represent the above equation in quadratic equation.
Detailed Solution: Question 11
Read the following text and answer the following questions on the basis of the same:
A small scale industry produces a certain boxes of candles in a day. Number of boxes prepared by each worked on a particular day was 2 more than thrice the number of workers working in the industry. The number of boxes produced in a particular day was 85.
Q. Number of workers working in the industry:
Detailed Solution: Question 12
Read the following text and answer the following questions on the basis of the same:
A small scale industry produces a certain boxes of candles in a day. Number of boxes prepared by each worked on a particular day was 2 more than thrice the number of workers working in the industry. The number of boxes produced in a particular day was 85.
Q. If the number of workers working in the industry is x. What was the number of boxes of candles prepared by each worker on that particular day?
Detailed Solution: Question 13
Read the following text and answer the following questions on the basis of the same:
A small scale industry produces a certain boxes of candles in a day. Number of boxes prepared by each worked on a particular day was 2 more than thrice the number of workers working in the industry. The number of boxes produced in a particular day was 85.
Q. Nature of roots of the above quadratic equation are:
Detailed Solution: Question 14
Read the following text and answer the following questions on the basis of the same:
A small scale industry produces a certain boxes of candles in a day. Number of boxes prepared by each worked on a particular day was 2 more than thrice the number of workers working in the industry. The number of boxes produced in a particular day was 85.
Q. How many boxes will be prepared when number of workers are increased by 2.
Detailed Solution: Question 15
118 videos|526 docs|45 tests |
