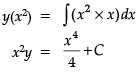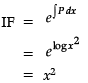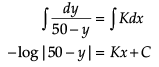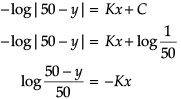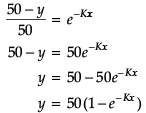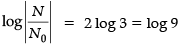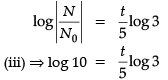Test: Differential Equations- Case Based Type Questions - Commerce MCQ
20 Questions MCQ Test - Test: Differential Equations- Case Based Type Questions
Direction: Read the following text and answer the following questions on the basis of the same:
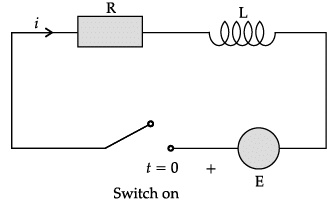
A differential equation of the form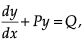 
where P and Q are functions of x alone, is called a first order linear differential equation. It has many applications in physics including RL circuits.
Consider the linear differential equation
Q. The general solution is _______.
where P and Q are functions of x alone, is called a first order linear differential equation. It has many applications in physics including RL circuits.
Direction: Read the following text and answer the following questions on the basis of the same:
A differential equation of the form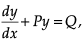 
where P and Q are functions of x alone, is called a first order linear differential equation. It has many applications in physics including RL circuits.
Consider the linear differential equation
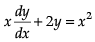
Q. The value of ∫ P dx = ______.
where P and Q are functions of x alone, is called a first order linear differential equation. It has many applications in physics including RL circuits.
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Direction: Read the following text and answer the following questions on the basis of the same:
A differential equation of the form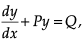 
where P and Q are functions of x alone, is called a first order linear differential equation. It has many applications in physics including RL circuits.
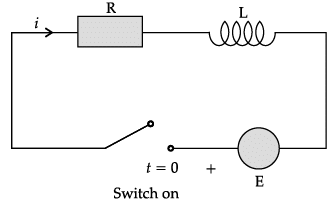
Consider the linear differential equation
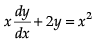
Q. ∫ Qdx = _______.
where P and Q are functions of x alone, is called a first order linear differential equation. It has many applications in physics including RL circuits.
Direction: Read the following text and answer the following questions on the basis of the same:
A differential equation of the form 
where P and Q are functions of x alone, is called a first order linear differential equation. It has many applications in physics including RL circuits.
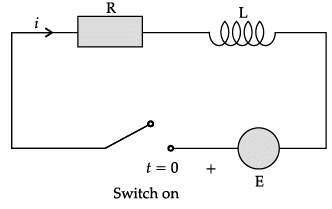
Consider the linear differential equation
Q. The integrating factor is _______.
Direction: Read the following text and answer the following questions on the basis of the same:
A differential equation of the form 
where P and Q are functions of x alone, is called a first order linear differential equation. It has many applications in physics including RL circuits.
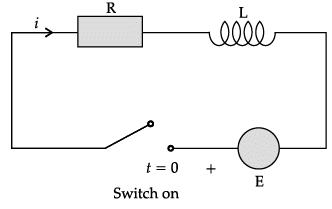
Consider the linear differential equation
Q. If y(1) = 0, then y(2) = _______.
Direction: Read the following text and answer the following questions on the basis of the same:
Polio drops are delivered to 50K children in a district. The rate at which polio drops are given is directly proportional to the number of children who have not been administered the drops. By the end of 2nd week half the children have been given the polio drops. How many will have been given the drops by the end of 3rd week can be estimated using the solution to the differential equation dy/dx = k(50 - y) where x denotes the number of weeks and y the number of children who have been given the drops.
Q. The value of C in the particular solution given that y(0) = 0 and k = 0.049 is
Direction: Read the following text and answer the following questions on the basis of the same:
Polio drops are delivered to 50K children in a district. The rate at which polio drops are given is directly proportional to the number of children who have not been administered the drops. By the end of 2nd week half the children have been given the polio drops. How many will have been given the drops by the end of 3rd week can be estimated using the solution to the differential equation dy/dx = k(50 - y) where x denotes the number of weeks and y the number of children who have been given the drops.
Q. Which method of solving a differential equation can be used to solve dy/dx = k(50 - y)?
Direction: Read the following text and answer the following questions on the basis of the same:
Polio drops are delivered to 50K children in a district. The rate at which polio drops are given is directly proportional to the number of children who have not been administered the drops. By the end of 2nd week half the children have been given the polio drops. How many will have been given the drops by the end of 3rd week can be estimated using the solution to the differential equation dy/dx = k(50 - y) where x denotes the number of weeks and y the number of children who have been given the drops.
Q. State the order of the above given differential equation.
Direction: Read the following text and answer the following questions on the basis of the same:
Polio drops are delivered to 50K children in a district. The rate at which polio drops are given is directly proportional to the number of children who have not been administered the drops. By the end of 2nd week half the children have been given the polio drops. How many will have been given the drops by the end of 3rd week can be estimated using the solution to the differential equation dy/dx = k(50 - y) where x denotes the number of weeks and y the number of children who have been given the drops.
Q. The solution of the differential equation dy/dx = k(50 - y) is given by,
Direction: Read the following text and answer the following questions on the basis of the same:
Polio drops are delivered to 50K children in a district. The rate at which polio drops are given is directly proportional to the number of children who have not been administered the drops. By the end of 2nd week half the children have been given the polio drops. How many will have been given the drops by the end of 3rd week can be estimated using the solution to the differential equation dy/dx = k(50 - y) where x denotes the number of weeks and y the number of children who have been given the drops.
Q. Which of the following solutions may be used to find the number of children who have been given the polio drops?
Direction: Read the following text and answer the following questions on the basis of the same:
A Veterinary doctor was examining a sick cat brought by a pet lover. When it was brought to the hospital, it was already dead. The pet lover wanted to find its time of death. He took the temperature of the cat at 11.30 pm which was 94.6°F. He took the temperature again after one hour; the temperature was lower than the first observation. It was 93.4°F. The room in which the cat was put is always at 70°F. The normal temperature of the cat is taken as 98.6°F when it was alive. The doctor estimated the time of death using Newton law of cooling which is governed by the differential equation: dT/dt ∞ (T−70), where 70°F is the room temperature and T is the temperature of the object at time t.
Substituting the two different observations of T and t made, in the solution of the differential equation dT/dt = k(T - 70) where k is a constant of proportion, time of death is calculated.
Q. The solution of the differential equation dT/dt = k(T - 70) is given by,
Direction: Read the following text and answer the following questions on the basis of the same:
A Veterinary doctor was examining a sick cat brought by a pet lover. When it was brought to the hospital, it was already dead. The pet lover wanted to find its time of death. He took the temperature of the cat at 11.30 pm which was 94.6°F. He took the temperature again after one hour; the temperature was lower than the first observation. It was 93.4°F. The room in which the cat was put is always at 70°F. The normal temperature of the cat is taken as 98.6°F when it was alive. The doctor estimated the time of death using Newton law of cooling which is governed by the differential equation: dT/dt ∞ (T−70), where 70°F is the room temperature and T is the temperature of the object at time t.
Substituting the two different observations of T and t made, in the solution of the differential equation dT/dt = k(T - 70) where k is a constant of proportion, time of death is calculated.
Q. Which method of solving a differential equation helped in calculation of the time of death?
Direction: Read the following text and answer the following questions on the basis of the same:
A Veterinary doctor was examining a sick cat brought by a pet lover. When it was brought to the hospital, it was already dead. The pet lover wanted to find its time of death. He took the temperature of the cat at 11.30 pm which was 94.6°F. He took the temperature again after one hour; the temperature was lower than the first observation. It was 93.4°F. The room in which the cat was put is always at 70°F. The normal temperature of the cat is taken as 98.6°F when it was alive. The doctor estimated the time of death using Newton law of cooling which is governed by the differential equation: dT/dt ∞ (T−70), where 70°F is the room temperature and T is the temperature of the object at time t.
Substituting the two different observations of T and t made, in the solution of the differential equation dT/dt = k(T - 70) where k is a constant of proportion, time of death is calculated.
Q. What will be the degree of the above given differential equation.
Direction: Read the following text and answer the following questions on the basis of the same:
A Veterinary doctor was examining a sick cat brought by a pet lover. When it was brought to the hospital, it was already dead. The pet lover wanted to find its time of death. He took the temperature of the cat at 11.30 pm which was 94.6°F. He took the temperature again after one hour; the temperature was lower than the first observation. It was 93.4°F. The room in which the cat was put is always at 70°F. The normal temperature of the cat is taken as 98.6°F when it was alive. The doctor estimated the time of death using Newton law of cooling which is governed by the differential equation: dT/dt ∞ (T−70), where 70°F is the room temperature and T is the temperature of the object at time t.
Substituting the two different observations of T and t made, in the solution of the differential equation dT/dt = k(T - 70) where k is a constant of proportion, time of death is calculated.
Q. If the temperature was measured 2 hours after 11.30 pm, what will be the change in time of death?
Direction: Read the following text and answer the following questions on the basis of the same:
A Veterinary doctor was examining a sick cat brought by a pet lover. When it was brought to the hospital, it was already dead. The pet lover wanted to find its time of death. He took the temperature of the cat at 11.30 pm which was 94.6°F. He took the temperature again after one hour; the temperature was lower than the first observation. It was 93.4°F. The room in which the cat was put is always at 70°F. The normal temperature of the cat is taken as 98.6°F when it was alive. The doctor estimated the time of death using Newton law of cooling which is governed by the differential equation: dT/dt ∞ (T−70), where 70°F is the room temperature and T is the temperature of the object at time t.
Substituting the two different observations of T and t made, in the solution of the differential equation dT/dt = k(T - 70) where k is a constant of proportion, time of death is calculated.
Q. If t = 0 when T is 72, then the value of C is
Direction: Read the following text and answer the following questions on the basis of the same:
The rate of increase in the number of bacteria in a certain bacteria culture is proportional to the number present. Given that the number triples in 5 hours.
Q. If N0 is the initial count of bacteria, after 10 hours the count is _______.
….(ii)
Direction: Read the following text and answer the following questions on the basis of the same:
The rate of increase in the number of bacteria in a certain bacteria culture is proportional to the number present. Given that the number triples in 5 hours.
Q. If ‘N’ is the number of bacteria, the corresponding differential equation is _______.
Direction: Read the following text and answer the following questions on the basis of the same:
The rate of increase in the number of bacteria in a certain bacteria culture is proportional to the number present. Given that the number triples in 5 hours.
Q. 
Direction: Read the following text and answer the following questions on the basis of the same:
The rate of increase in the number of bacteria in a certain bacteria culture is proportional to the number present. Given that the number triples in 5 hours.
Q. The general solution is _______.
Direction: Read the following text and answer the following questions on the basis of the same:
The rate of increase in the number of bacteria in a certain bacteria culture is proportional to the number present. Given that the number triples in 5 hours.
Q. The bacteria becomes 10 times in _______ hours.
Top Courses for Commerce
Important Questions for Differential Equations- Case Based Type Questions
Differential Equations- Case Based Type Questions MCQs with Answers
Online Tests for Differential Equations- Case Based Type Questions
|
© EduRev
|
Education Revolution
|
|
