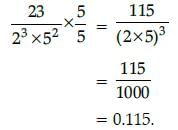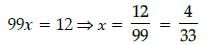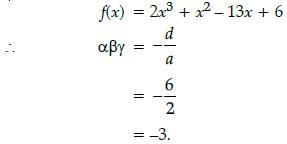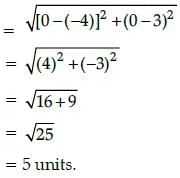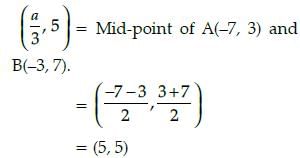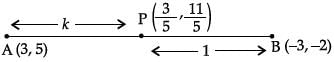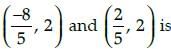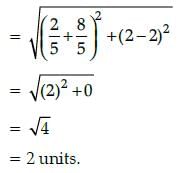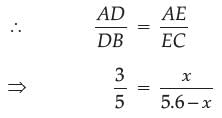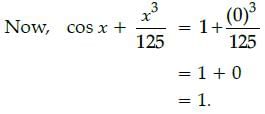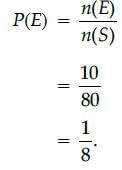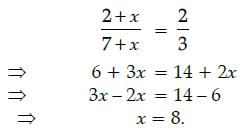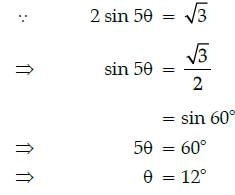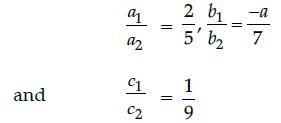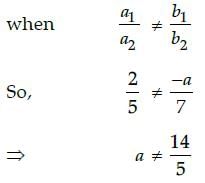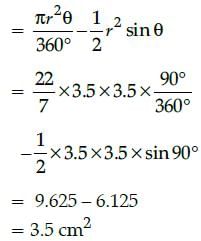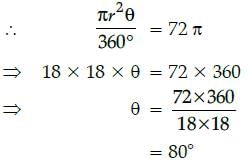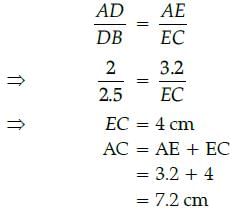Test: Class 10 Mathematics: CBSE Sample Question Paper- Term I (2021-22) - Class 10 MCQ
30 Questions MCQ Test - Test: Class 10 Mathematics: CBSE Sample Question Paper- Term I (2021-22)
The product of two numbers is 1900 and their LCM is 100, then the HCF of the numbers is:
If a number when divided by 71 gives 37 as quotient and 42 as remainder, then the number is:
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
The decimal expansion of the rational number 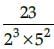 will terminate after:
will terminate after:
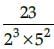 will terminate after:
will terminate after:The number 0.121212 ...... is the form of p/q will be equal:
If the sum of the zeroes of the quadratic polynomial 5x2 – px + 8 is 4, then the value of k is:
If the polynomial is p(x) = x3 - 3x2 + x + 1, then the value of p(- 3) is:
If α, β and γ are the zeroes of the polynomial 2x3 + x2 – 13x + 6, then abg is equal to:
The distance of the point P(– 4, 3) from the origin is:
If 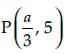 is the mid point of the line segment joining the points A(–7, 3) and B(– 3, 7), then the value of a is:
is the mid point of the line segment joining the points A(–7, 3) and B(– 3, 7), then the value of a is:
The point 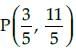 divide the line segment joining the points A(3, 5) and (– 3, – 2) is the ratio:
divide the line segment joining the points A(3, 5) and (– 3, – 2) is the ratio:
The distance between the points 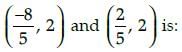
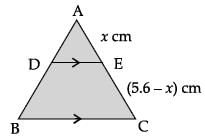
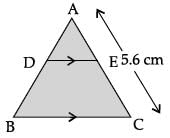
In a given ABC, DE || BC and AB/DB = 3/5. If AC = 5.6 cm, then AE = .
If sin A = 1/√2, then the value of tan A + cot A is:
If x = 0, then the value of 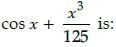
The value of sin2 30° – cos2 30° is:
The circumference of a circle of radius 4 cm is: (Use π = 3.14)
Aarti had bought a circular pot wherein area of cross-section is mentioned as 38.5 cm2. She wantedto calculate the radius of the circle and observed its value.
If a piece of wire 30 cm long is bent into the form of an arc of a circle, subtending an angle of 60° at its centre, then radius of the circle is :
Which of the following can not be the probability of an event ?
A box contains 80 discs, numbered from 1 to 90. If one disc is drawn at random from the box, the probability that it bears a prime number less than 30, is:
What number must be added to numerator and denominator of 2/7 to make fraction equal to 2/3 ?
The difference of LCM and HCF of 28 and 42 is:
If the sum of ages of father and son is 40 years and its difference is 20 years then age of father will be:
If 2 sin 5θ = √3, then the value of q is:
The system of equations 2x + ay = 1 and 5x – 7y = 9 are given.
If the system has a unique solution, then all real values except :
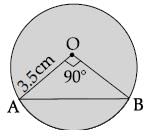
If the radius of a circle with centre O is 3.5 cm and two radii OA and OB are drawn at right angles toeach other, then the area of minor segment is :
If the area of a sector of the circle of radius 18 cm is 72π cm2, then the angle q is :
The zeroes of the quadratic polynomial 3x2 + 2x – 1 = 0 are :
In the given figure, if PQ = 8 cm and PR = 6 cm, then the radius of the circle is ..... cm, where O is thecentre of circle.

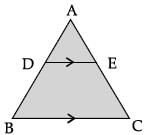
In the given figure, If DE || BC, AD = 2 cm, BD = 2.5 cm, AE = 3.2 cm and DE = 4 cm, then BC = 9 cmFind AC.