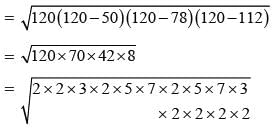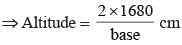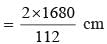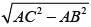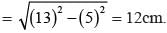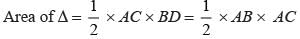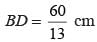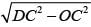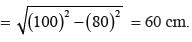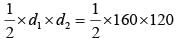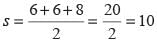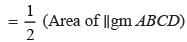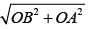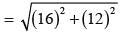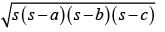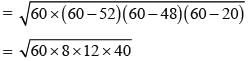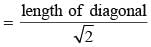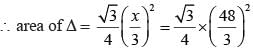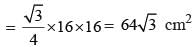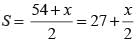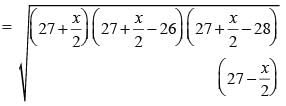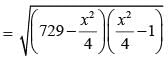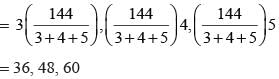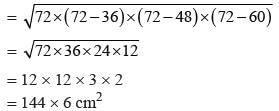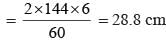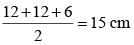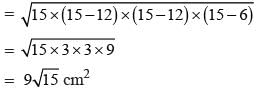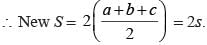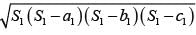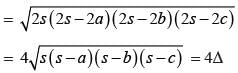Math Olympiad Test: Heron’s Formula- 2 - Class 9 MCQ
15 Questions MCQ Test - Math Olympiad Test: Heron’s Formula- 2
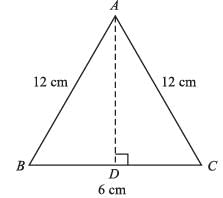
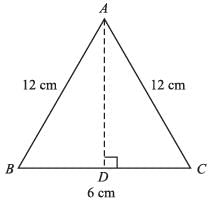
The area of an isosceles triangles whose equal sides are 12cm and the other side is 6cm long, will be:
The sides of a triangle are 50 cm, 78 cm and 112 cm. the smallest altitude is:
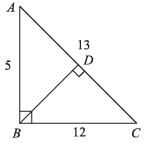
The base and hypotenuse of a right triangle are 5 cm, 13 cm long. The length of altitude from the vertex containing right angle to the hypotenuse will be:
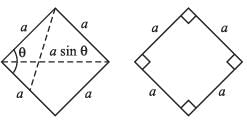
If a square and rhombus have same perimeter, and area of square is S and area of rhombus is R, then
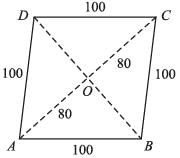
The area of kite in the adjoining figure is: (AC = BD = 32 cm)
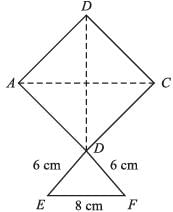
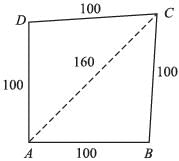
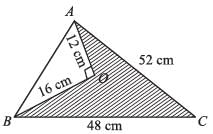
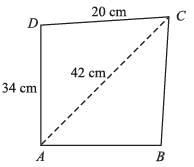
Area of parallelogram, in the adjoining figure will be:
A square and an equilateral triangle have equal perimeters. If the diagonal of the square is 12√2 cm, the area of the triangle is:
The third side of triangle whose two sides are 26 and 28 cm and area is 336 cm2, is
The length of sides of a triangle are in the ratio 3 : 4 : 5 and its perimeter is 144 cm, then, the height corresponding to the length side is:
ABCD is a parallelogram, where,
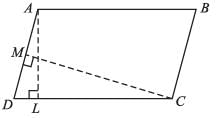
AL = 8 cm, CM = 10 cm, AD = 6 cm. Find AB.
If each side of ∆ is doubled, then the area will become how many times?
The diagonal of a parallelogram divide it in 2 parts, the area of the two parts:


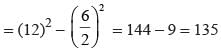
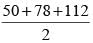 = 120 cm
= 120 cm