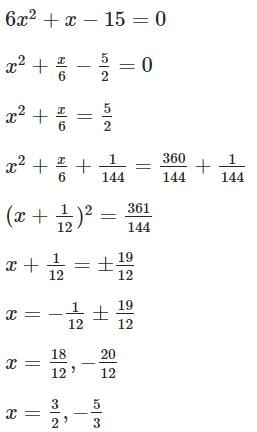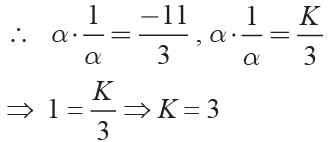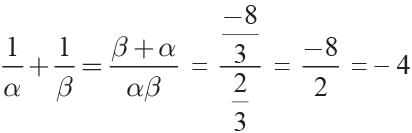Math Olympiad Test: Quadratic Equations- 1 - Class 10 MCQ
10 Questions MCQ Test - Math Olympiad Test: Quadratic Equations- 1
The area of a square is 169 cm2. What is the length of one side of the square?
A right triangle has a side with length 12 in and a hypotenuse with length 20 in. Find the length of the second leg. (Round to the nearest hundredth if needed)
Find the x-intercepts for the following equation.
Y = 6x2 - 7x - 3
Y = 6x2 - 7x - 3
Use the quadratic formula to find the values of x for the equation:
x2 - 4x - 10 = 0
Which statement best describes the solutions to the equation below?
3x2 - 5x + 20 = 0
If -5, is a root of the quadratic equation 2x2 + Px - 15 = 0 and the quadratic equation P (x2 +x) + K = 0 has equal roots. What is the value of K?
If one root of 3x2 + 11x +K = 0 is reciprocal of the other then what is the value of K?
If α, β are the roots of the equation 3x2 + 8x + 2 = 0 then the value of (1/α + 1/β) is