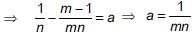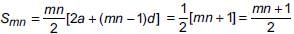Math Olympiad Test: Arithmetic Progression- 3 - Class 10 MCQ
10 Questions MCQ Test - Math Olympiad Test: Arithmetic Progression- 3
Find the sum of first 20 terms of an A.P. whose nth term is given by Tn = (7 – 3n).
If 9th term of an A.P. is zero, then its 29th term is ________ its 19th term.
Which term of the A.P. 5, 2, –1, ....... is –22?
In an A. P., the sum of first n terms is 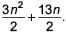 Find its 25th term.
Find its 25th term.
In an A.P., if the pth term is ‘q’ and the qth term is ‘p’, then its nth term is ________.
The sum of all terms of the arithmetic progression having ten terms except for the first term, is 99, and except for the sixth term, is 89. Find the 8th term of the progression if the sum of the first and the fifth term is equal to 10.
The ratio of the sum of m and n terms of an A.P. is m2 : n2, then find the ratio of mth and nth terms.
If x ≠ y and the sequences x, a1, a2, y and x, b1, b2, y each are in A.P., then 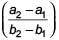 is ________.
is ________.
If the mth term of an A.P. is 1/n and nth term is 1/m, then the sum of first mn terms is _______.
Four numbers are inserted between the numbers 4 and 39 such that an A.P. results. Find the biggest of these four numbers.



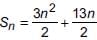
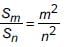
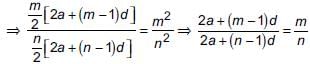
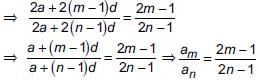
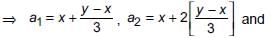

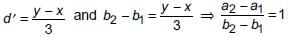

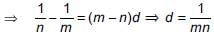
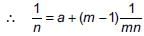 [From (i)]
[From (i)]