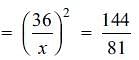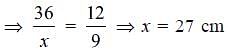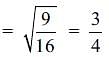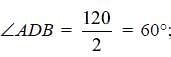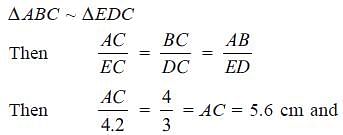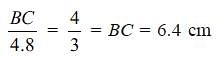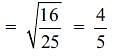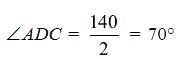Test Level 1: Geometry - 2 - CAT MCQ
20 Questions MCQ Test - Test Level 1: Geometry - 2
A vertical stick 20 m long casts a shadow 10 m long on the ground. At the same time, a tower casts the shadow 50 m long on the ground. Find the height of the tower.
The area of similar triangles, ABC and DEF are 144 cm2 and 81 cm2 respectively. If the longest side of larger ΔABC be 36 cm, then the longest side of smaller ΔDEF is
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
The areas of two similar Ds are respectively 9 cm2 and 16 cm2. Find the ratio of their corresponding sides.
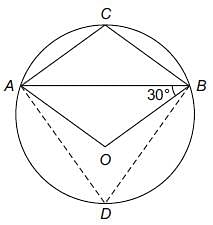
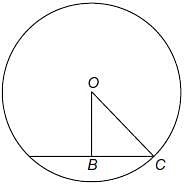
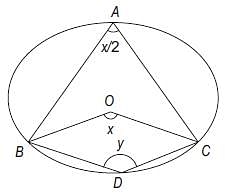
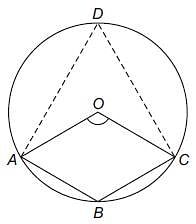
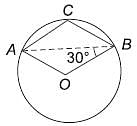
In the following figure, O is the centre of the circle and ∠ABO = 30°, find ∠ACB.
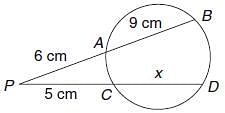
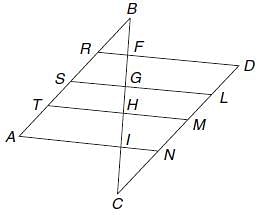
In the figure, AB is parallel to CD and RD | | SL || TM || AN, and BR : RS : ST : TA = 3 : 5 : 2 : 7. If it is known that CN = 1.333 BR. Find the ratio of BF : FG : GH : HI : IC
In the figure, DABC is similar to DEDC.
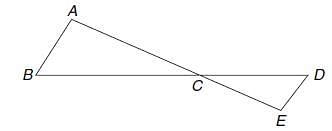
If we have AB = 4 cm,
ED = 3 cm, CE = 4.2 and
CD = 4.8 cm, find the value of CA and CB
Two isosceles Ds have equal angles and their areas are in the ratio 16 : 25. Find the ratio of their corresponding heights.
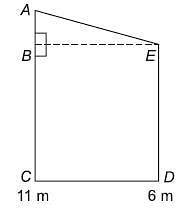
Two poles of height 6 m and 11 m stand vertically upright on a plane ground. If the distance between their foot is 12 m, find the distance between their tops.
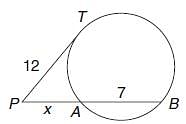
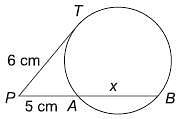
Find the length of a chord that is at a distance of 12 cm from the centre of a circle of radius 13 cm.
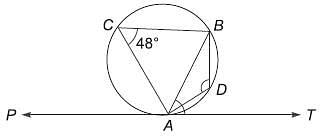
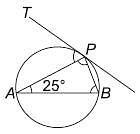
In the given figure AB is the diameter of the circle and ∠PAB = 25°. Find ∠TPA.
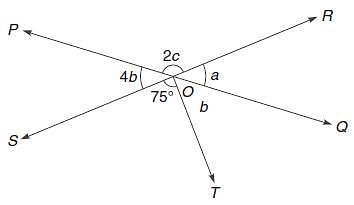
In the given figure, two straight lines PQ and RS intersect each other at O. If ∠SOT = 75°, find the value of a, b and c.
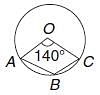
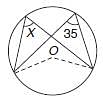
In the following figure, it is given that o is the centre of the circle and ∠AOC = 140°. Find ∠ABC.