Test Level 2: Speed, Time and Distance - 2 - CAT MCQ
20 Questions MCQ Test - Test Level 2: Speed, Time and Distance - 2
A, B and C take part in a race over a distance of d metres at uniform speed. If A can beat B by 20 metres, B can beat C by 10 metres and A can beat C by 28 metres, then what is the value of d?
Mr. Racer started from Hyderabad to Bangalore with a speed of 60 kmph. After some time, he changed his speed to 80 kmph and reached Bangalore. He returned with the same speed and changed his speed to 60 kmph at the place where he had initially changed his speed in the onward journey, and came back to Hyderabad. What was his average speed for the entire journey? (The distance between Hyderabad and Bangalore is 600 km).
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
A boat P travels 40 km upstream from point A to point B in 10 hours and from point B to point A downstream in 5 hours. Another boat Q can travel from point A to a point C, 30 km upstream, in 5 hours. At 10 am, P starts from A and goes towards B. At the same time, Q starts from C and goes towards A.
At what time will they meet each other?
Ramesh takes 6 hours for a 300 km journey from Pune to Mumbai, if 180 km is travelled by train and the rest by bike. It takes 15 minutes more, if 200 km is travelled by train and the rest by bike. The ratio of the speed of the train to that of the bike is
Mani leaves home for office at 7 a.m. and reaches at 7:40 a.m. On the other hand, his brother Vikram leaves the same office at 7:20 a.m. and reaches their common home at 7:50 am. At what time do they cross on the way, if they follow the same route?
A ship develops a leak 12 km from the shore. Despite the leak, the ship is able to move towards the shore at a speed of 8 km/hr. However, the ship can stay afloat only for 20 minutes. If a rescue vessel were to leave from the shore towards the ship and it takes 4 minutes to evacuate the crew and passengers of the ship, what should be the minimum speed of the rescue vessel in order to be able to successfully rescue the people aboard the ship?
Two guns are fired from the same place at an interval of 12 minutes, but a person in a train approaching the place hears the second shot 10 minutes after the first. Find the speed of the train if the speed of sound is 330 m/s.
A boat P travels 40 km upstream from point A to B in 10 hours and from point B to A downstream in 5 hours. Another boat Q can travel from point A to a point C 30 km upstream in 5 hours. At 10 am, P starts from A and goes towards B. At the same time, Q starts from C and proceeds towards A. At what distance from B will they meet each other?
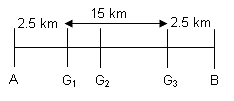
In a 20 km long tunnel connecting two cities A and B, there are three gutters. The distance between gutters 1 and 2 is half the distance between gutters 2 and 3. The distance from city A to its nearest gutter - gutter 1 - is equal to the distance of city B from gutter 3. On a particular day, the hospital in city A receives information that an accident has occurred at the third gutter. The victim can be saved only if an operation is started within 40 minutes. An ambulance starts from city A at 30 km/hr and crosses the first gutter after 5 minutes. If the driver doubles the speed after that, then what is the maximum amount of time the doctor will get to attend the patient at the hospital before starting the operation. Assume 1 minute elapses in taking the patient into and out of the ambulance.
The J&K Express from Delhi to Srinagar was delayed by snowfall for 16 minutes and made up for the delay on a section of 80 km travelling with a speed 10 km per hour higher than its normal speed. Find the original speed of the J&K Express (according to the schedule)
Amitabh covered a distance of 96 km two hours faster than he had planned to. This he achieved by travelling 1 km more every hour than he intended to cover every 1 hour 15 minutes. What was the speed at which Amitabh travelled during the journey?
A pedestrian and a cyclist start simultaneously towards each other from Aurangabad and Paithan which are 40 km apart and meet 2 hours after the start. Then they resumed their trips and the cyclist arrives at Aurangabad 7 hours 30 minutes earlier than the pedestrian arrives at Paithan. Which of these could be the speed of the pedestrian?
Two motorists met at 10 a.m. at the Dadar railway station. After their meeting, one of them proceeded in the East direction while the other proceeded in the North direction. Exactly at noon, they were 60 km apart. Find the speed of the slower motorist if the difference of their speeds is 6 km/h.
Two ants start simultaneously from two ant holes towards each other. The first ant coveres 8% of the distance between the two ant holes in 3 hours, the second ant covered 7/120 of the distance in 2 hours 30 minutes. Find the speed (feet/h) of the second ant if the first ant travelled 800 feet to the meeting point.
A racetrack is in the form of a right triangle. The longer of the legs of the track is 2 km more than the shorter of the legs (both these legs being on a highway). The start and end points are also connected to each other through a side road. The escort vehicle for the race took the side road and rode with a speed of 30 km/h and then covered the two intervals along the highway during the same time with a speed of 42 km/h. Find the length of the racetrack.
Karim, a tourist leaves Ellora on a bicycle. Having travelled for 1.5 h at 16 km/h, he makes a stop for 1.5 h and then pedals on with the same speed. Four hours after Karim started, his friend and local guide Rahim leaves Ellora on a motorcycle and rides with a speed of 28 km/h in the same direction as Karim had gone. What distance will they cover before Rahim overtakes Karim?
An ant climbing up a vertical pole ascends 12 meters and slips down 5 meters in every alternate hour. If the pole is 63 meters high how long will it take it to reach the top?
An ant moved for several seconds and covered 3 mm in the first second and 4 mm more in each successive second than in its predecessor. If the ant had covered 1 mm in the first second and 8 mm more in each successive second, then the difference between the path it would cover during the same time and the actual path would be more than 6 mm but less than 30 mm. Find the time for which the ant moved (in seconds).
The Sabarmati Express left Ahmedabad for Mumbai. Having travelled 300 km, which constitutes 66.666 per cent of the distance between Ahmedabad and Mumbai, the train was stopped by a red signal. Half an hour later, the track was cleared and the enginedriver, having increased the speed by 15 km per hour, arrived at Mumbai on time. Find the initial speed of the Sabarmati Express.
Read the following and answer the question that follow.
A naughty bird is sitting on top of a car. It sees another car approaching it at a distance of 12 km. The speed of the two cars is 60 kmph each. The bird starts flying from the first car and moves towards the second car, reaches the second car and comes back to the first car and so on. If the speed at which the bird flies is 120 kmph then answer the following questions. Assume that the two cars have a crash.
Q. The total distance travelled by the bird before the crash is


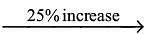 speed per 75 minutes
speed per 75 minutes 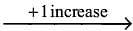 New speed.
New speed. Speed per 75 minutes
Speed per 75 minutes  We need to use this process to check the option.
We need to use this process to check the option.