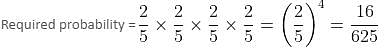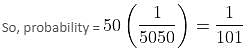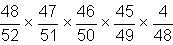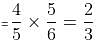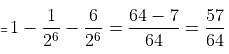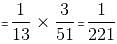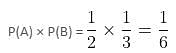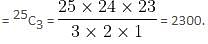Test Level 2: Probability - 2 - CAT MCQ
20 Questions MCQ Test - Test Level 2: Probability - 2
If four whole numbers taken at random are multiplied together, find the probability that the last digit in the product is 1, 3, 7, or 9.
The numbers 1, 2, 3, …., 100 are written on 100 cards with one number on each card. The cards are placed in a hat and one card is selected. The sizes and shapes of the cards are such that the probability of selecting the card labelled with the number 'n' is equal to 'n' times the probability of selecting the card labelled 1. What is the probability that the card labelled 50 is selected?
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Cards are drawn one by one from a deck of 52 cards without replacement. What is the probability that four cards are drawn before the first ace (fifth card) is drawn?
Find the probability that a leap year selected at random contains either 53 Sundays or 53 Mondays.
A candidate is to be selected for an interview for two posts. The number of candidates for the first post is 5 and that for the second post is 6. Find the probability of getting at least one job.
Two cards are drawn in succession from a pack of 52 cards. The first card should be a Queen and the second should be a King. What is the probability of doing so if the first card is replaced?
Six unbiased coins are tossed simultaneously. Find the probability that at least two heads occur.
Two numbers a and b are chosen at random from the set of first 30 natural numbers. The probability that a2 - b2 is divisible by 3 is
A bag contains 5 square boxes and 7 cylindrical boxes. Two boxes are drawn at random. Find the probability that they are the same shape.
Consider a pack of 52 cards. One card is drawn at random. What is the probability of the card being a heart or a seven?
Two cards are drawn one by one at random without replacement from a pack of 52 cards. What is the probability that the cards drawn are queens?
Two fair dice are thrown. What is the probability that the number of dots on the first dice is greater than 3 and that on the second is greater than 4?
In a room, there are 15 men and 10 women. Three of them are selected at random. The probability that 1 woman and 2 men are selected is
In a box, there are 5 red, 9 green and 6 black balls. One ball is picked up randomly. What is the probability that it is neither red nor green?
In a simultaneous throw of a pair of dice, find the probability of getting an even number on one and a multiple of 3 on the other.
A bag contains 4 yellow balls, 5 green balls and 3 red balls. What is the probability of drawing a red or a yellow ball?
There are two dice; red and green. What is the probability that on roll the red die throws up a prime number which is divisible by the number thrown up on the roll of the green die?
Two fair dices are thrown. Given that the sum of the dice is less than or equal to 4, find the probability that only one dice shows two.
There are two bags, one of them contains 5 red and 7 white balls and the other 3 red and 12 white balls, and a ball is to be drawn from one or the other of the two bags. Find the chance of drawing a red ball.
If 8 coins are tossed, what is the chance that one and only one will turn up Head?