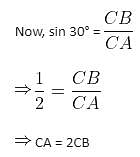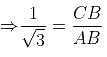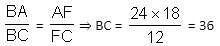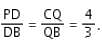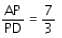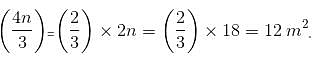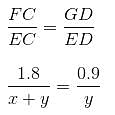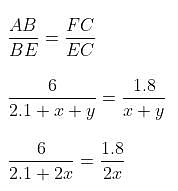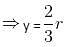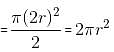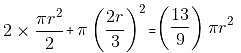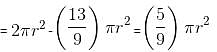Test Level 2: Geometry - 2 - CAT MCQ
20 Questions MCQ Test - Test Level 2: Geometry - 2
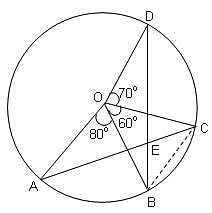
If segments AB, BC and CD subtend angles of 80°, 60° and 70°, respectively, at the centre O of a circle, then the measure of an acute angle between AC and BD would be _____.
In the given figure, O is the centre of the circle, ∠BOC = 70° and AB is perpendicular to OC. Find the measure of angle OCA.

| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
What is the smallest possible radius of a circle such that it is possible to place 6 points on its circumference with an integral distance between any two adjacent points?
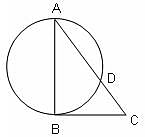
In the given figure, AB is a diameter of the circle, line BC is tangent to the circle, ∠BAC = 30° and length of CD = √3 units. Find the radius of the circle.
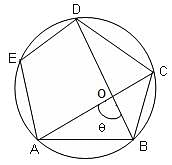
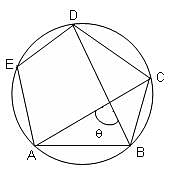
ABCDE is a regular pentagon inscribed in the given circle. What is the measure of the acute angle θ between AC and BD?
In the given figure, if AC is a diameter of the circle and the angles CAD, BAC, BCA and ACD form an arithmetic progression with angle CAD = 15°, then which of the following options is the measure of angle BCA?
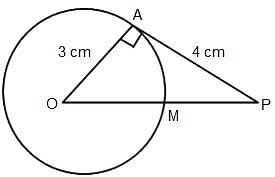
A tangent to a circle of radius 3 cm from an external point P is of length 4 cm. Find the shortest distance of point P from a point on the circumference of the circle.
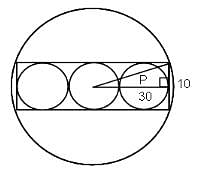
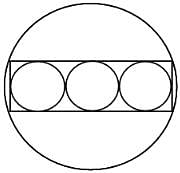
Three circles, each with a radius of 10 cm, are drawn tangent to one another so that their centres are all in a straight line. These circles are inscribed in a rectangle which is inscribed in another circle. The area of the largest circle is ________.
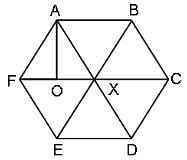
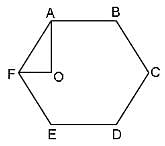
In the figure, ABCDEF is a regular hexagon and ∠AOF = 90°. FO is parallel to ED. What is the ratio of the area of the triangle AOF to that of the hexagon ABCDEF?
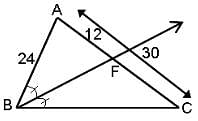
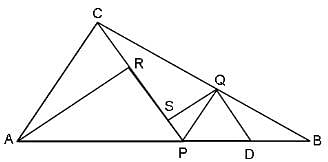
In the figure (not drawn to scale), P is a point on AB such that AP : PB = 4 : 3. PQ is parallel to AC and QD is parallel to CP. In ΔARC, ∠ARC = 90° and in ΔPQS, ∠PSQ = 90°. The length of QS is 6 cm. What is the ratio of AP : PD?
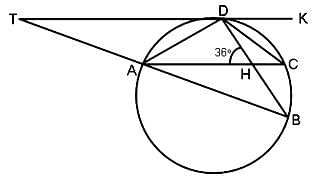
In the figure given below, AB is a diameter of the circle, TD is a tangent to the circle and AB = 2AD. If AHD = 36° and DBA = 30°, then what is the measure of CDT?
What is the maximum number of dogs that can be tied in a spherical hall such that all the dogs are equidistant from each other?
In the diagram given below,
∠ABC = 90° = ∠DCH = ∠DOE = ∠EHK = ∠FKL = ∠GLM = $∠LMN
AB = BC = 2CH = 2CD = EH = FK = 2HK = 4KL = 2LM = MN
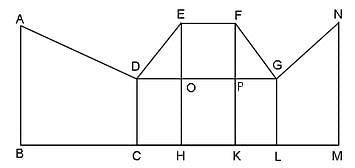
What is the measure of ∠FGO?
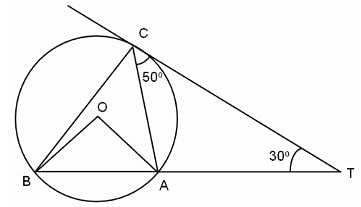
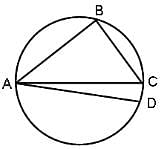
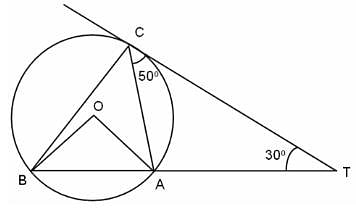
In the figure (not drawn to scale), A, B and C are three points on a circle with centre O. The chord BA is extended to a point T, such that CT becomes a tangent to the circle at point C. If ∠ATC = 30° and ∠ACT = 50°, find the measure of angle ∠BOA.
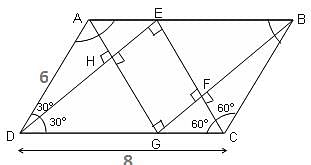
The bisectors of the four angles of a parallelogram are drawn. An acute angle of the parallelogram is 60° and the adjacent sides are 8 and 6 units. What is the area of the quadrilateral whose vertices are the points of intersection of the bisectors?
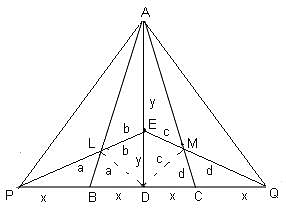
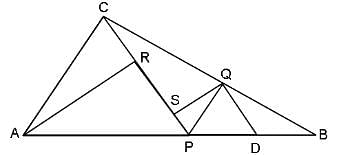
Let E be the midpoint of median AD of ABC. Let DB be produced to P, such that DB = BP and let DC be produced to Q, such that DC = CQ. Let EP cuts AB at L and EQ cuts AC at M. What is the area of pentagon BLEMC, if area of ABC is 18 m2?
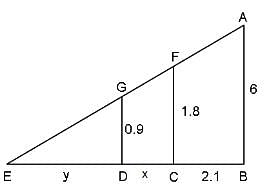
A father and his son were waiting at a bus stop in the evening. There was a lamp post behind them. The lamp post, the father and his son stood on the same straight line. The father observed that the shadows of his head and his son's head were incident at the same point on the ground. If the heights of the lamp post, the father and his son were 6 m, 1.8 m and 0.9 m, respectively, and the father was standing 2.1 m away from the post, then how far (in m) was the son standing from his father?
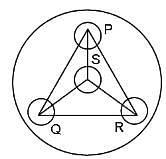
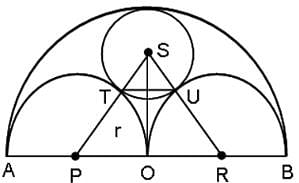
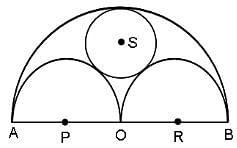
Three horses are grazing within a semi-circular field as shown in the diagram and AB is the diameter of the semi-circular field with centre at O. The horses are tied up at P, R and S such that PO and RO are the radii of semicircles with centres at P and R, respectively and S is the centre of the circle touching the two semi-circles with diameters AO and OB. The horses tied at P and R can graze within the respective semi-circles and the horse tied at S can graze within the circle centred at S. What is the percentage of area of the semi-circle with diameter AB that cannot be grazed by the horses?
The circumference of a circle equals the perimeter of a triangle of equal sides and also the perimeter of a square. The areas covered by the circle, the triangle and the square are c, t and s, respectively. Which of the following relations is true?