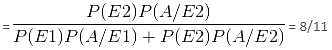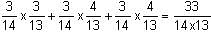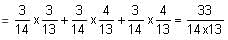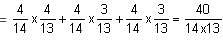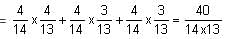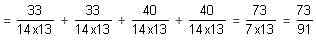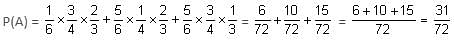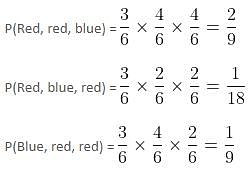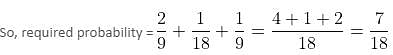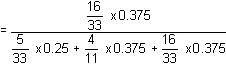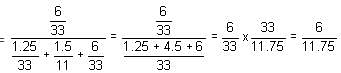Test Level 3: Probability - 2 - CAT MCQ
10 Questions MCQ Test - Test Level 3: Probability - 2
Suppose a girl throws a die. If she gets a 5 or 6, she tosses a coin three times and notes the number of heads. If she gets a 1, 2, 3 or 4, she tosses a coin once and notes whether a head or tail is obtained. If she obtained exactly one head, what is the probability of getting a 1, 2, 3 or 4 on the die?
Two balls are drawn at random from a bag containing 3 white, 3 red, 4 green and 4 black balls one by one without replacement. Find the probability that both the balls are of different colours.
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
The probabilities that three men hit a target are 1/6, 1/4 and 1/3. Each man shoots once at the target. What is the probability that exactly one of them hits the target?
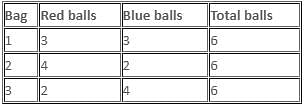
Three bags contain 18 balls of red and blue colours. The first bag contains 3 red and 3 blue balls. The second bag contains 4 red and 2 blue balls and the third bag contains 2 red and 4 blue balls. One ball is taken out at random from each bag. The probability of getting 2 red balls and 1 blue ball is
In a tailor shop, tailor A makes 500 shirts, tailor B makes 1200 shirts and tailor C makes 1600 shirts. Out of these, 200, 300 and 300 shirts are defective, respectively. One shirt is drawn at random and if it is found to be defective, then the probability that is made by tailor C is
Directions: Study the following information and answer the given question.
Three friends A, B and C do air rifle shooting as a hobby and compete against each other in friendly competitions. On a Sunday morning, they go to an empty tract of land along with their air rifles to shoot at clay practice targets from the distances of 100 m and 200 m. A hits his target 95% of the times from a distance of 100 m and 70% times from a distance of 200 m. The same figures for B are 85% and 80%, respectively. The same figures for C are 90% and 75%, respectively. They put in numbered chits (1, 2 and 3) to be drawn to decide the order of shooting and then each of them shoots at the targets turn-wise according to the chit number, first from 100 m and then from 200 m. They decide on a point system with 1 point for hitting the target from a distance of 100 m and 2 points for hitting it from a distance of 200 m with the winner getting a round of drinks paid by the other two.
Q. What is the probability that the order of shooting is ABC?
Directions: Study the following information and answer the given question.
Three friends A, B and C do air rifle shooting as a hobby and compete against each other in friendly competitions. On a Sunday morning, they go to an empty tract of land along with their air rifles to shoot at clay practice targets from the distances of 100 m and 200 m. A hits his target 95% of the times from a distance of 100 m and 70% times from a distance of 200 m. The same figures for B are 85% and 80%, respectively. The same figures for C are 90% and 75%, respectively. They put in numbered chits (1, 2 and 3) to be drawn to decide the order of shooting and then each of them shoots at the targets turn-wise according to the chit number, first from 100 m and then from 200 m. They decide on a point system with 1 point for hitting the target from a distance of 100 m and 2 points for hitting it from a distance of 200 m with the winner getting a round of drinks paid by the other two.
Q. What is the probability that all three of them will end up shooting 1 target only, with all three of them shooting the target of the same points weightage?
A bag X contains 3 white and 2 black balls. Another bag Y contains 2 white and 4 black balls. A bag and a ball out of it are picked at random. Find the probability that the ball is of white colour.
Directions: Read the given information and answer the following:
Two friends A and B play a game of chance. A person tosses a coin and if the coin shows a heads, he rolls a die. He does this twice and the score is the total of the numbers that the die throws up in both the rolls, if at all. If a person ends up with a tails on tossing the coin, he does not roll the die and his score is entered as 0. The winner of the game is the person whose score is the maximum.
Q. What is the probability that A wins the game with a score of 2 and B ends up with a score of 0?
Directions: Read the given information and answer the following:
Two friends A and B play a game of chance. A person tosses a coin and if the coin shows a heads, he rolls a die. He does this twice and the score is the total of the numbers that the die throws up in both the rolls, if at all. If a person ends up with a tails on tossing the coin, he does not roll the die and his score is entered as 0. The winner of the game is the person whose score is the maximum.
Q. What is the probability that A ends up with an odd score without scoring a 0 in any of his rolls?