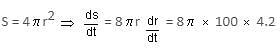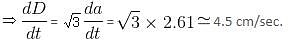Test Level 2: Functions - 2 - CAT MCQ
20 Questions MCQ Test - Test Level 2: Functions - 2
Let f(x) = 7x3 + 23x + 18. If the value of f(x + 8) - f(x + 7) - f(x + 6) + f(x + 5) - f(x + 4) + f(x + 3) + f(x + 2) - f(x + 1) is a constant, then find that value.
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Let f(x) = x5 + ax4 + bx3 + cx2 + dx + e and f(1) = f(2) = f(3) = f(4) = f(5). Then a is equal to
If f(x) = (x5 - 1) (x3 + 1), g(x) = (x2 - 1) (x2 - x + 1) and h(x) is a polynomial such that f(x) = g(x)h(x), what is the value of h(1)?
Consider a recursive function C defined by:
C(n, 0) = n + 1
C(0, i) = C(1, i - 1) for i > 0
C(n, i) = C(C(n -1, i), ( i - 1)) for n > 0 and i > 0
Compute C(1, 2) from the above definition.
Let f and g be functions and f(g(x)) = x + 2 and f(s) = 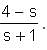 . What is the value of g(t)?
. What is the value of g(t)?
Let f(x) = 1 - 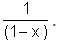 Find f(f(f(…f(4)..))), when there are 1997 f's in the composition.
Find f(f(f(…f(4)..))), when there are 1997 f's in the composition.
The value of the function f(n) is 35/16 which is represented as f(n) = 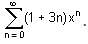 Find the value of x(Answer upto one decimal place).
Find the value of x(Answer upto one decimal place).
If f(x + y) = f(x) + f(y) and f(1) + f(2) + f(3) … f(10) = 1, find the value of f(1).
If f is a function such that f(0) = 2, f(1) = 3 and f(x + 2) = 2f(x) - f(x + 1), then f(5) is equal to
If the graph of y = f(x) is transformed to the graph of 2y - 6 = -4f(x - 3), point (a, b) on the graph of y = f(x) becomes point (A, B) on the graph of 2y - 6 = -4f(x - 3), where A and B are given by:
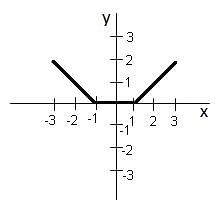
Given below is a graph made up of line segments shown as thick lines. Which of the following options is correct?
The graphs of f(x) and g(x) are shown below:
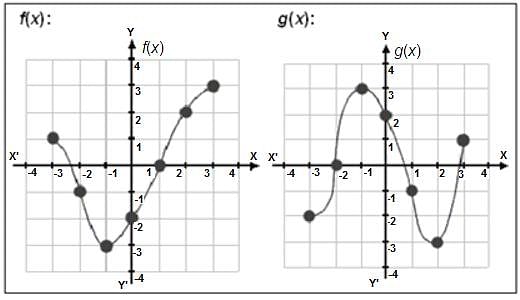
Find (fog)(-1).
A sphere's radius is increasing at the rate of 4.2 cm/sec. Find the rate at which its area of surface changes when the radius is 100 cm.
A cube's edge is changing at the rate of 2.61 cm/sec. The rate of change of its longest diagonal will be (approx.)
A large company intends to maximise its profits using calculus. Its unit sales price is Rs. 500 and cost of production = 100 + 5X2, where X is the total units sold or produced. Find the most profitable production level.
A company sells its products at Rs. 155 per kg and its cost of manufacture is given by Rs. (X2 + 5) per kg. Find the production level for maximum profit, if X = production level.
In Indore, Annapurna area has 2000 telephone subscribers and government collects fixed charges of Rs. 280 per month from each subscriber. The government proposes to increase the tariff and if it is forecasted for each rupee increase, there will be an equivalent amount of subscribers discontinuing. So, what increase will bring maximum revenue to the government?
The maximum area of a rectangle with perimeter equal to 12 units will be
Let f1(n) = n - 28 n 6
f2(m) = m - 16 ≤ m - 1
f(x) = f(m) + f(n)
What is the value of fmax(x) and fmin(x)?


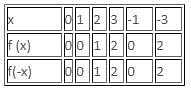
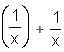 f(-x) = 2x, what is the value of f(2)?
f(-x) = 2x, what is the value of f(2)?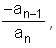 , we get that the sum of the roots of f(x) - A is - a.
, we get that the sum of the roots of f(x) - A is - a.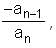 , we mean that the polynomial may have "multiple" roots and we are to count the roots with multiplicity. For example, (x - 1)2 (x - 2)3 = x5 - 8x4 + …. Where 8 represents the sum of the roots counting 1 twice and 2 thrice.)
, we mean that the polynomial may have "multiple" roots and we are to count the roots with multiplicity. For example, (x - 1)2 (x - 2)3 = x5 - 8x4 + …. Where 8 represents the sum of the roots counting 1 twice and 2 thrice.)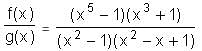
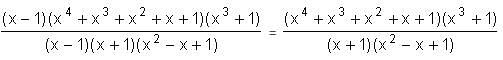
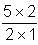 = 5.
= 5.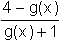
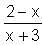
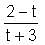
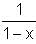
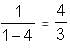
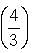 = 1 -
= 1 -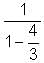 = 4.
= 4.