Test Level 3: Inequalities - CAT MCQ
10 Questions MCQ Test - Test Level 3: Inequalities
The total money that Vijay (V) and Manju (M) have is less than Rs. 5 but both are having some money. Which of the following is not necessarily true?
How many ordered pairs of natural numbers satisfy the inequality 8x + 2y ≤ 24?
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
If b > a and c < 0, then which of the following is true (a, b > 0)?
If -1 ≤ v ≤ 1, -2 ≤ u ≤ -0.5, -2 ≤ z ≤ -0.5 and w = vz/u, then which of the following is necessarily true?
If - 2 ≤ a ≤ - 1, - 4 ≤ b ≤ - 2, 2 ≤ c ≤ 4 and 1 ≤ d ≤ 3, what is the maximum value of ab2/cd2 ?
For the given consecutive integers p, q, r and s, such that, p, q, r, s > 0, then, which of the following can be true?
Which of the following is the possible value of a in the given inequality |2a + 3| > |7a - 2|?
To determine their favourite brand of chocolates in a particular community, a big chain of retail stores conducted a survey for elementary school kids. In the survey, a kid was presented with a tray of 8 chocolates of different brands and asked to pick one. In all, 400 kids were involved in the survey. Out of the first 100, 20 chose brand C. In the next 200, 40 chose brand C. k kids in the last 100 opted for brand C. If not more than 25% of kids chose brand C, then which of the following inequalities best describes the value for k?
For the given pair (x, y) of positive integers, 7x + 3y = 123. How many integral pairs of x and y satisfy the given condition?
x and y are real numbers satisfying the conditions 2 < x < 3 and - 8 < y < - 7. Which of the following expressions will have the least value?


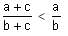

 which is true.
which is true.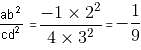
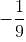
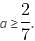
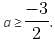
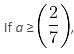 then inequality becomes,
then inequality becomes,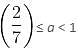
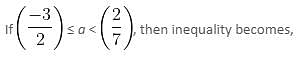
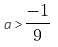
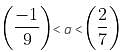
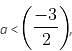 then inequality becomes,
then inequality becomes,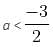
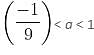 is the correct interval of a.
is the correct interval of a.














