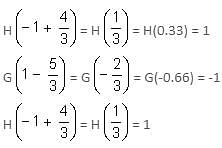Test Level 3: Functions - CAT MCQ
10 Questions MCQ Test - Test Level 3: Functions
If f(x) = xa + ax and g(x) = xa - ax , then find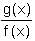 , when x = 2 and a = 3.
, when x = 2 and a = 3.
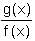 , when x = 2 and a = 3.
, when x = 2 and a = 3.| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
When f(x) - f(-x) = 0, the function f(x) is called an even function. Which of the following functions is an even function?
A function satisfies f(0, n) = n + 1 and f(m + 1, n) = f(m, f(m, n)). What is the value of f(4, 100)?
If f(x) satisfies 2f(x) + f(1 – x) = x2 for all x, then f(x) is equal to
Let f(x) be a polynomial with integer coefficients, for which 3 and 13 are the roots. Which of the following could possibly be the value of f(10)?
A function f(x) is called even if f(-x) = f(x) for all x and it is called odd if f(-x) = -f(x) for all x. Which of the following statements is/are true?
(i) The product of an even function and an odd function is even.
(ii) The sum of two even functions is even.
(iii) The product of two odd functions is even.
For all real numbers x, a function f(x) satisfies 2f(x) + f(1 - x) = x2. Find the value of f(5).
Refer to the following data to answer the question that follows.
F(x) = Modulus of x
G(x) = The largest integer less than or equal to x
H(x) = The smallest integer greater than or equal to x
I(x) = x, a real number
Find the value of H
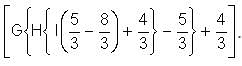


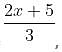 then f -1(x) = ?
then f -1(x) = ?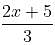
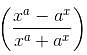

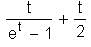 … (1)
… (1)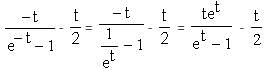
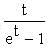 (1 - et) + t = -t + t = 0
(1 - et) + t = -t + t = 0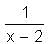 ?
?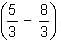 = I (-1) = -1
= I (-1) = -1