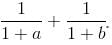Test Level 1: Quadratic Equations & Linear Equations - 1 - CAT MCQ
10 Questions MCQ Test - Test Level 1: Quadratic Equations & Linear Equations - 1
Total integer pair(s) (x, y) satisfying the equation x + y = xy is/are
If A = 2 and B + P + F = 24, what are the values of Q and S? Consider whole numbers only.
A + B = Z, Z + P = T, T + A = F, F + S = Q, Q - T = 7
A + B = Z, Z + P = T, T + A = F, F + S = Q, Q - T = 7
Which of the following is the correct value of x for the equation 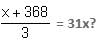
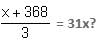
Let x and y be real numbers, such that (x2 - y2)(x2 - 2xy + y2) = 3 and x - y = 1. What is the value of xy?
If p, q and r are the roots of the cubic equation x3 - 3x2 + 5x + k = 2 and pqr = 1, then find the value of k.
Find the value of x3 + y3 + z3 - 3xyz when x + y + z = 9 and xy + yz + zx = 11.
If (a2 + b2)3 = (a3 + b3)2, then find the value of 
1/2 (a + b + c){(a - b)2 + (b - c)2 + (c - a)2} is equal to
What is the value of y if 1/x + 2/y = 3/z ?
If x = ay and y = bx, where the values of x and y cannot be zero, find the value of