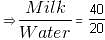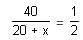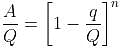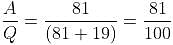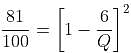Test Level 1: Mixtures and Alligations - CAT MCQ
10 Questions MCQ Test - Test Level 1: Mixtures and Alligations
In a mixture of 60 litres, the ratio of milk to water is 2 : 1. If the ratio of milk to water needs to be 1 : 2, then the amount of water (in litres) to be added further is
If 20 litres of mixture containing 15% alcohol is mixed with 30 litres of mixture containing 18% alcohol, what is the concentration of the resulting solution?
A milkman mixes 20 litres of water with 80 litres of milk. After selling one-fourth of this mixture, he adds water to replenish the quantity that he has sold. What is the current proportion of water to milk?
A vessel is full of a mixture of liquor and water with 18% liquor. Eight litres are drawn of and then the vessel is filled with water. How much does the vessel hold if the liquor is now 15%?
Six gallons of wine is drawn from a cask and is replaced by six gallons of water. Six gallons of the mixture is drawn and again replaced by six gallons of water. If the ratio of wine to water in the cask is now 81 : 19, then how much wine was in the cask at first?
We have two solutions of milk - A and B. Solution A contains milk and water in the ratio of 1 : 3 and solution B contains the same in the ratio of 2 : 3. If we mix both in equal quantities, then what is the ratio of milk and water in the new solution?
A lump of two metals weighing 18 grams is worth Rs. 74, but if their weights are interchanged, it would be worth Rs. 60.10. If the price of gold is Rs. 7.20 per gram, then find the weight of the other metal in the mixture.
We have two solutions of milk - A and B. Solution A contains milk and water in the ratio of 1 : 3 and solution B contains the same in the ratio of 2 : 3. If we mix both in equal quantities, then what is the ratio of milk and water in the new solution?
An alloy contains zinc and tin in the ratio of 3 : 4. Another alloy contains zinc and silver in the ratio of 4 : 3. If both of these alloys are melted and mixed in equal ratios, then what will be the ratio of zinc and tin in the new alloy?
Two liquids A and B are in the ratio 5 : 1 in container X and in the ratio 1 : 3 in container Y. In what ratio should the contents of the two containers be mixed so as to obtain a mixture of A and B in the ratio 1 : 1?