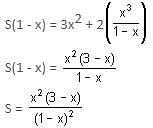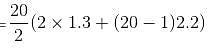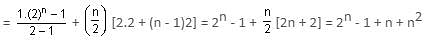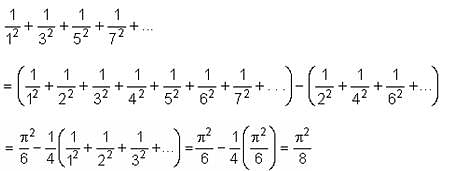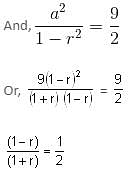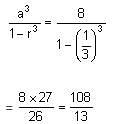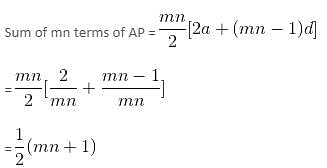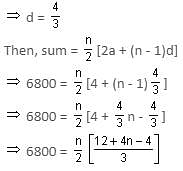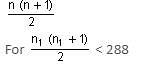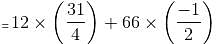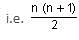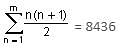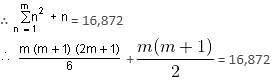Test Level 2: Progressions, Sequences & Series - 2 - CAT MCQ
20 Questions MCQ Test - Test Level 2: Progressions, Sequences & Series - 2
Find the sum: 3x2 + 5x3 + 7x4 + 9x5 + .............
1.3 + 3.5 + 5.7 + ... (up to 20 terms) is equal to
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Find the sum of the series: 1 + 3 + 5 + 6 + 9 + 12 + 13 + .......... (10 terms)
If a, b and c are in AP, then 1/bc, 1/ca and 1/ab are in
Find the sum of the following series up to n terms:
3 + 6 + 10 + 16 + …
Let a1, a2, a3... be in an A.P with a common difference, which is not a multiple of 3. The maximum number of consecutive terms which are in AP and are also prime numbers, is
A radio set manufacturer produced 600 units in the third year and 700 units in the seventh year. Assuming that the production uniformly increases by a fixed number every year, find (i) the production in the first year (ii) the production in the 10th year and (iii) the total production in 7 years.
If the sum of an infinitely decreasing G.P. is 3 and the sum of squares of its terms is 9/2, then the sum of cubes of its terms is _____.
In an AP, the mth term is 1/n and the nth term is 1/m. The sum of first mn terms is
The first term of an arithmetic progression is 2 and the fourth term is 6. If the sum of first n terms of the progression is 6800, find the value of n.
If the sums of first 8 and 19 terms of an AP are 64 and 361, respectively, then the sum of its first n terms will be
Find the 5th term of an HP, if the sum of the reciprocals of the first nine terms of the harmonic progression is 90.
If the sum of the first 11 terms of an AP equals the sum of the first 19 terms, then what is the sum of the first 30 terms?
The 288th term of the series abbcccddddeeeeefffffff.... is
The number of terms between 30 and 530, which are divisible by 11, is
Find the sum of all natural numbers between 250 and 1000, which are exactly divisible by 3.
In an AP, S4 = 28 and S8 = 48. Find S12.
The sum of five numbers in an AP is 30 and the sum of their squares is 220. Find the numbers.
There are 8436 steel balls, each of radius 1 cm, stacked in a pile with 1 ball at the top, 3 balls in the second layer, 6 in the third layer, 10 in the fourth, and so on. The number of horizontal layers in the pile will be