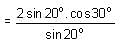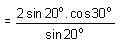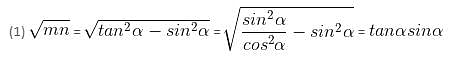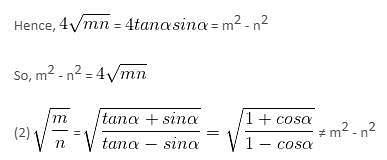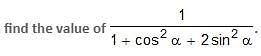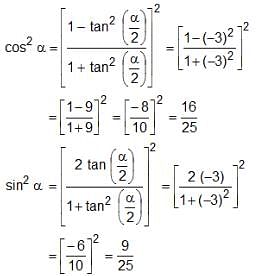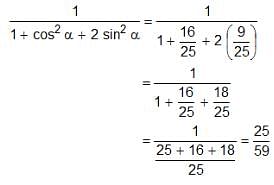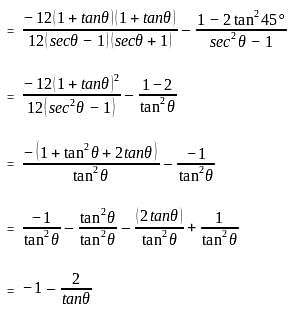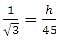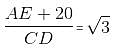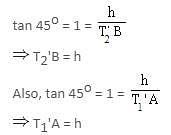Test Level 2: Trigonometry - 2 - CAT MCQ
15 Questions MCQ Test - Test Level 2: Trigonometry - 2
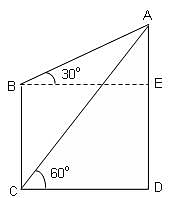
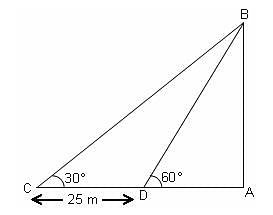
The length of the shadow of a vertical pole on level ground increases by 25 metres when the altitude of the sun changes from 60° to 30°. Calculate the height of the pole.
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
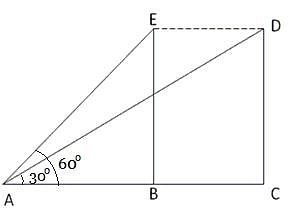
The angles of elevation of a plane flying at a constant altitude of 10000 ft are found to be 60° and 30° at an interval of 1 minute. What is the speed of the plane?
If 4 cos2 A + 2 sin2 A = 3, then what is the value of A, given that A lies in the first quadrant?
AB is a vertical pole. The end A is on the level ground and C is the middle point of AB. P is a point on the level ground. The portion BC subtends an angle β at P. If AP = nAB, then tan equals
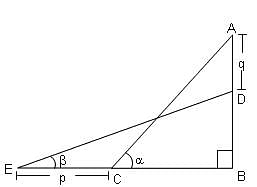
A ladder rests against a vertical wall at an inclination α to the horizontal. Its foot is pulled away from the wall through a distance p, such that its upper end slides a distance q down the wall and then the ladder makes an angle β to the horizontal.
What is the value of P/q?
If tan α + sin α = m and tan α - sin α = n, then m2 - n2 =
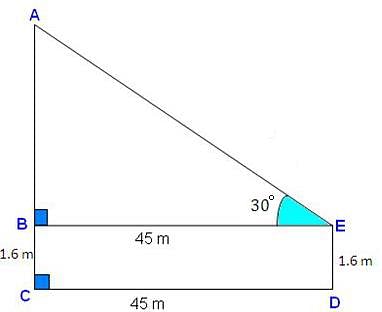
A 1.6 m tall observer is 45 meters away from a tower. If the angle of elevation from his eye to the top of the tower is 30°, then the height of the tower in meters is
(Take √3 = 1.732)
The angle of elevation of the top of a tower from a point on the ground at some distance from its base is 60°. The angle of elevation of the top of the tower from a point 20 m above the same point on the ground is 30°. What is the height of the tower?
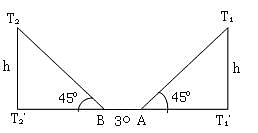
Two vertical poles of equal height are 120 m apart. On the line joining their bases, A and B are two points. Angle of elevation of the top of one pole from A is 45o and that of the other pole from B is also 45o. If AB = 30 m, then the height of each pole is



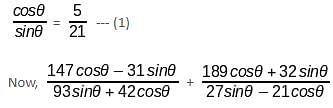
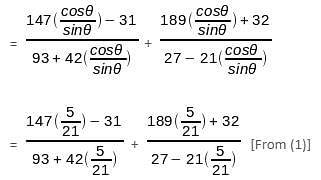
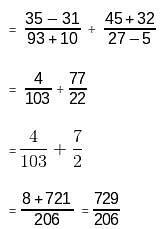
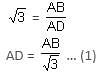

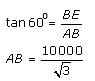
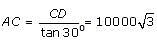
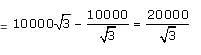
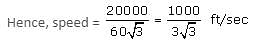
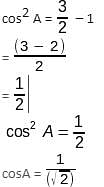

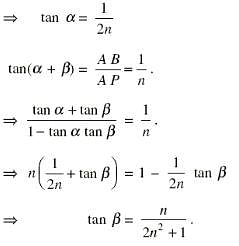
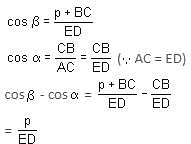
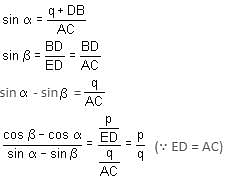
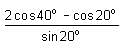
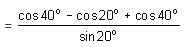
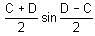
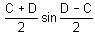 ]
]
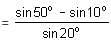
 ]
]