All Courses
Get the App Signup / Login
Sign in Open App
Bank Exams Exam  >  Bank Exams Tests  >  Test: Quantitative Aptitude - 2 - Bank Exams MCQ

Test: Quantitative Aptitude - 2 - Bank Exams MCQ


Test Description

20 Questions MCQ Test - Test: Quantitative Aptitude - 2

Test: Quantitative Aptitude - 2 for Bank Exams 2024 is part of Bank Exams preparation. The Test: Quantitative Aptitude - 2 questions and answers have been prepared according to the Bank Exams exam syllabus.The Test: Quantitative Aptitude - 2 MCQs are made for Bank Exams 2024 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests for Test: Quantitative Aptitude - 2 below.
Solutions of Test: Quantitative Aptitude - 2 questions in English are available as part of our course for Bank Exams & Test: Quantitative Aptitude - 2 solutions in Hindi for Bank Exams course. Download more important topics, notes, lectures and mock test series for Bank Exams Exam by signing up for free. Attempt Test: Quantitative Aptitude - 2 | 20 questions in 10 minutes | Mock test for Bank Exams preparation | Free important questions MCQ to study for Bank Exams Exam | Download free PDF with solutions
Test: Quantitative Aptitude - 2 - Question 1
Save

Directions: Read the following information carefully and answer the questions based on it.

An adhesive manufacturing company formed adhesives by mixing five chemicals – C1, C2, C3, C4, and C5 in different proportions. Chart given below shows the cost price per liter of these five chemicals.

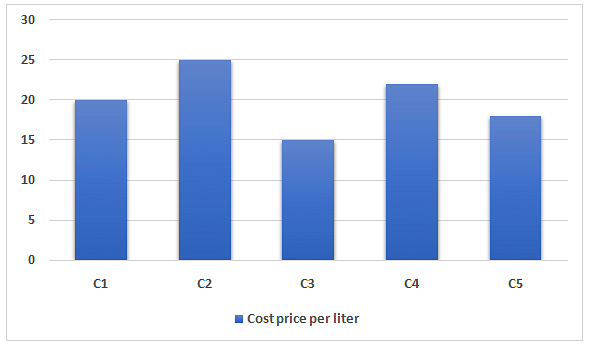
  • C4 formed by mixing C1 and C2 in equal proportion, while C5 formed by mixing C1 and C3 in equal proportion.
  • Adhesive 1 (AD1) formed by mixing C2 and C3 in 30% and 70% proportion respectively, while AD2 formed by mixing C4 and C5 in equal proportions.
  • Adhesive 3 (AD3) formed by mixing C3 and C4 in equal proportion, while AD 4 formed by mixing C1 and C5 in 2:1.

Q. Which of the following can be the possible cost per liter of Adhesive 2 (AD 2).

I. Rs. 20

II. Rs. 19.25

III. Rs. 20.25

IV. Rs. 19.75

Detailed Solution for Test: Quantitative Aptitude - 2 - Question 1

Cost per liter of C1 = Rs. 20

Cost per liter of C2 = Rs. 25

Cost per liter of C3 = Rs. 15

Cot per liter of C4 = Rs. 22

C4 also be formed by mixing C1 and C2 in equal proportion

So, Cost per liter of C4 = 1/2 x 20 + 1/2 x 25 = Rs. 22.50

Cost per liter of C4 = Rs. 18

C5 also formed by mixing C1 and C3 in equal proportion

Cost per liter of C5 = 1/2 x 20 + 1/2 x 15 = Rs. 17.5

According to Question,

AD2 formed by mixing C4 and C5 in equal proportions.

Cost per liter of C4 = Rs. 22 and Rs. 22.5

Cost per liter of C5 = Rs. 18 and Rs. 17.5

Possible cost per liter of AD2

= 1/2 x 22 + 1/2 x 18 = Rs. 20

= 1/2 x 22 + 1/2 x 17.5 = Rs. 19.75

= 1/2 x 22.5+ 1/2 x 18 = Rs. 20.25

= 1/2 x 22.5 + 1/2 x 17.5 = Rs. 20

Only I, III, IV follows

Hence answer is option D

Test: Quantitative Aptitude - 2 - Question 2
Save

Directions: Read the following information carefully and answer the questions based on it.

An adhesive manufacturing company formed adhesives by mixing five chemicals – C1, C2, C3, C4, and C5 in different proportions. Chart given below shows the cost price per liter of these five chemicals.

  • C4 formed by mixing C1 and C2 in equal proportion, while C5 formed by mixing C1 and C3 in equal proportion.
  • Adhesive 1 (AD1) formed by mixing C2 and C3 in 30% and 70% proportion respectively, while AD2 formed by mixing C4 and C5 in equal proportions.
  • Adhesive 3 (AD3) formed by mixing C3 and C4 in equal proportion, while AD 4 formed by mixing C1 and C5 in 2:1.

Q. Find cost price per liter of Adhesive 1 (AD1)?

Detailed Solution for Test: Quantitative Aptitude - 2 - Question 2

Cost per liter of C1 = Rs. 20

Cost per liter of C2 = Rs. 25

Cost per liter of C3 = Rs. 15

Cot per liter of C4 = Rs. 22

C4 also be formed by mixing C1 and C2 in equal proportion

So, Cost per liter of C4 = 1/2 x 20 + 1/2 x 25 = Rs. 22.50

Cost per liter of C4 = Rs. 18

C5 also formed by mixing C1 and C3 in equal proportion

Cost per liter of C5 = 1/2 x 20 + 1/2 x 15 = Rs. 17.5

Adhesive 1 (AD1) formed by mixing C2 and C3 in 30% and 70% proportion respectively.

Required cost price per liter = 3/10 x 25 + 7/10 x 15 = Rs. 18/liter

Hence answer is option B

1 Crore+ students have signed up on EduRev. Have you? Download the App
Test: Quantitative Aptitude - 2 - Question 3
Save

Directions: Read the following information carefully and answer the questions based on it.

An adhesive manufacturing company formed adhesives by mixing five chemicals – C1, C2, C3, C4, and C5 in different proportions. Chart given below shows the cost price per liter of these five chemicals.

  • C4 formed by mixing C1 and C2 in equal proportion, while C5 formed by mixing C1 and C3 in equal proportion.
  • Adhesive 1 (AD1) formed by mixing C2 and C3 in 30% and 70% proportion respectively, while AD2 formed by mixing C4 and C5 in equal proportions.
  • Adhesive 3 (AD3) formed by mixing C3 and C4 in equal proportion, while AD 4 formed by mixing C1 and C5 in 2:1.

Detailed Solution for Test: Quantitative Aptitude - 2 - Question 3

Cost per liter of C1 = Rs. 20

Cost per liter of C2 = Rs. 25

Cost per liter of C3 = Rs. 15

Cot per liter of C4 = Rs. 22

C4 also be formed by mixing C1 and C2 in equal proportion

So, Cost per liter of C4 = 1/2 x 20 + 1/2 x 25 = Rs. 22.50

Cost per liter of C4 = Rs. 18

C5 also formed by mixing C1 and C3 in equal proportion

Cost per liter of C5 = 1/2 x 20 + 1/2 x 15 = Rs. 17.5

A3 can be formed by formed C3 and C4 in equal proportion.

So, a liter of A3 contains a/2 liters of each of C3 and C4

C4 formed by mixing equal proportion of C1 and C2 in equal proportion.

So, a/2 liters of C4 contains a/4 liters of each C1 and C2.

So A3 = a/4 (C1) + a/4 (C2) + a/2 (C3)

C1: C2: C3 = a/4: a/4: a/2 = 1:1:2

Hence answer is option D

Test: Quantitative Aptitude - 2 - Question 4
Save

Directions: Read the following information carefully and answer the questions based on it.

An adhesive manufacturing company formed adhesives by mixing five chemicals – C1, C2, C3, C4, and C5 in different proportions. Chart given below shows the cost price per liter of these five chemicals.

  • C4 formed by mixing C1 and C2 in equal proportion, while C5 formed by mixing C1 and C3 in equal proportion.
  • Adhesive 1 (AD1) formed by mixing C2 and C3 in 30% and 70% proportion respectively, while AD2 formed by mixing C4 and C5 in equal proportions.
  • Adhesive 3 (AD3) formed by mixing C3 and C4 in equal proportion, while AD 4 formed by mixing C1 and C5 in 2:1.

Q. Find cost price per liter of Adhesive AD4, if company makes maximum profit on selling AD4?
Detailed Solution for Test: Quantitative Aptitude - 2 - Question 4

Cost per liter of C1 = Rs. 20

Cost per liter of C2 = Rs. 25

Cost per liter of C3 = Rs. 15

Cot per liter of C4 = Rs. 22

C4 also be formed by mixing C1 and C2 in equal proportion

So, Cost per liter of C4 = 1/2 x 20 + 1/2 x 25 = Rs. 22.50

Cost per liter of C4 = Rs. 18

C5 also formed by mixing C1 and C3 in equal proportion

Cost per liter of C5 = 1/2 x 20 + 1/2 x 15 = Rs. 17.5

If company makes Maximum profit, then cost price should be minimum to earn maximum profit

AD4 formed by mixing C1 and C5 in 2:1 ratio.

Cost price per liter of C1 = Rs. 20

Cost price per liter of C5 = Rs. 18 and Rs. 17.5

Required minimum cost = 2/3 x 20 + 1/3 x 17.5 = Rs. 19.17/liter

Hence answer is option B

Test: Quantitative Aptitude - 2 - Question 5
Save

Directions: Read the following information carefully and answer the questions based on it.

The following bar graph shows the number of employees and number of managers working in a company as on 31st December of different years. The company was started in 2010 and from then 1/5thof the employees and 1/4th of managers who joined the company in any year leave the company after exactly two years and no other employee leaves at any other time.

Total employees in company = Managers + Non – Managers

It is also known that 12 employees left in 2016 and 8managers left in 2014. In 2017 as well as 2019, all the employees who left were managers.

Q. Find the number of managers joined in 2018?
Detailed Solution for Test: Quantitative Aptitude - 2 - Question 5

It is known that 12 employees left in 2016

Let number of employees joined in 2016 = K

434 + K – 12 = 492

K = 70 (Number of employees joined in 2016

1/5 of number of employees those joined, leaves exactly after two years, so

1/5 of number of employees joined in 2014 = 12

Number of employees joined in 2014 = 12 x 5 = 60

Similarly in 2018 number of employees joined = 612 + 1/5 of 70 – 586 = 40

(70 employees those joined in 2016, 1/5 of them left in 2018)

It is known that 8managers left in 2014

So, number of managers joined in 2014 = 204 + 8 – 164 = 48

25% of managers those joined, leaves exactly after 2 years. So,

25% of managers joined in 2012 = 8

Number of managers joined in 2012 = 4 x 8 = 32

Number of managers joined in 2016 = 230 + 25% of48 –210 = 32

(48managers those joined in 2018, 25% of them left in 2016)

Let the number of employees left in 2017 = a = number of managers left in 2017

Let number of employees left in 2019 = b = number of managers left in 2019

Number of employees joined in 2017 = 586 + a – 492 = 94 + a

Number of managers those joined in 2017 = 304 + a – 230 = 74 + a

So, 20% of (94+ a) = 25% of (74 + a)

376 + 4a = 370 + 5a

So, a = 6

So, number of employees joined in 2017 = 94 + 6 = 100

Number of managers joined in 2017 = 74 + 6 = 80

Also, 20% of number of employees joined in 2015 = a = 6

Number of employees joined in 2015 = 6 x 5 = 30

25% of managers joined in 2015 = a = 6

Number of managers joined in 2015 = 6 x 4 = 24

Also, number of employees left in 2015 = 438 + 30 – 434 = 34

Number of managers left in 2011 = 204 + 24 – 210 = 18

20% of number of employees joined in 2013 = 34 (number of employees left in 2015)

Number of employees joined in 2013 = 34 x 5 = 170

25% of managers joined in 2013 = 18

Number of managers joined in 2013 = 18 x 4 = 72

The following table gives number of employees joined each year

According to question,

Number of managers joined in 2018 = 32

Hence answer is option C

Test: Quantitative Aptitude - 2 - Question 6
Save

Directions: Read the following information carefully and answer the questions based on it.

The following bar graph shows the number of employees and number of managers working in a company as on 31st December of different years. The company was started in 2010 and from then 1/5thof the employees and 1/4th of managers who joined the company in any year leave the company after exactly two years and no other employee leaves at any other time.

Total employees in company = Managers + Non – Managers

It is also known that 12 employees left in 2016 and 8managers left in 2014. In 2017 as well as 2019, all the employees who left were managers.

Q. In which of the years from 2013 to 2018, did the maximum number of employees join the company?
Detailed Solution for Test: Quantitative Aptitude - 2 - Question 6

It is known that 12 employees left in 2016

Let number of employees joined in 2016 = K

434 + K – 12 = 492

K = 70 (Number of employees joined in 2016

1/5 of number of employees those joined, leaves exactly after two years, so

1/5 of number of employees joined in 2014 = 12

Number of employees joined in 2014 = 12 x 5 = 60

Similarly in 2018 number of employees joined = 612 + 1/5 of 70 – 586 = 40

(70 employees those joined in 2016, 1/5 of them left in 2018)

It is known that 8managers left in 2014

So, number of managers joined in 2014 = 204 + 8 – 164 = 48

25% of managers those joined, leaves exactly after 2 years. So,

25% of managers joined in 2012 = 8

Number of managers joined in 2012 = 4 x 8 = 32

Number of managers joined in 2016 = 230 + 25% of48 –210 = 32

(48managers those joined in 2018, 25% of them left in 2016)

Let the number of employees left in 2017 = a = number of managers left in 2017

Let number of employees left in 2019 = b = number of managers left in 2019

Number of employees joined in 2017 = 586 + a – 492 = 94 + a

Number of managers those joined in 2017 = 304 + a – 230 = 74 + a

So, 20% of (94+ a) = 25% of (74 + a)

376 + 4a = 370 + 5a

So, a = 6

So, number of employees joined in 2017 = 94 + 6 = 100

Number of managers joined in 2017 = 74 + 6 = 80

Also, 20% of number of employees joined in 2015 = a = 6

Number of employees joined in 2015 = 6 x 5 = 30

25% of managers joined in 2015 = a = 6

Number of managers joined in 2015 = 6 x 4 = 24

Also, number of employees left in 2015 = 438 + 30 – 434 = 34

Number of managers left in 2011 = 204 + 24 – 210 = 18

20% of number of employees joined in 2013 = 34 (number of employees left in 2015)

Number of employees joined in 2013 = 34 x 5 = 170

25% of managers joined in 2013 = 18

Number of managers joined in 2013 = 18 x 4 = 72

The following table gives number of employees joined each year

From table, maximum (170) employees joined in 2013.

Hence answer is option B

Test: Quantitative Aptitude - 2 - Question 7
Save

Directions: Read the following information carefully and answer the questions based on it.

The following bar graph shows the number of employees and number of managers working in a company as on 31st December of different years. The company was started in 2010 and from then 1/5thof the employees and 1/4th of managers who joined the company in any year leave the company after exactly two years and no other employee leaves at any other time.

Total employees in company = Managers + Non – Managers

It is also known that 12 employees left in 2016 and 8managers left in 2014. In 2017 as well as 2019, all the employees who left were managers.

Q. Find number of non – managers joined in 2017?
Detailed Solution for Test: Quantitative Aptitude - 2 - Question 7

It is known that 12 employees left in 2016

Let number of employees joined in 2016 = K

434 + K – 12 = 492

K = 70 (Number of employees joined in 2016

1/5 of number of employees those joined, leaves exactly after two years, so

1/5 of number of employees joined in 2014 = 12

Number of employees joined in 2014 = 12 x 5 = 60

Similarly in 2018 number of employees joined = 612 + 1/5 of 70 – 586 = 40

(70 employees those joined in 2016, 1/5 of them left in 2018)

It is known that 8managers left in 2014

So, number of managers joined in 2014 = 204 + 8 – 164 = 48

25% of managers those joined, leaves exactly after 2 years. So,

25% of managers joined in 2012 = 8

Number of managers joined in 2012 = 4 x 8 = 32

Number of managers joined in 2016 = 230 + 25% of48 –210 = 32

(48managers those joined in 2018, 25% of them left in 2016)

Let the number of employees left in 2017 = a = number of managers left in 2017

Let number of employees left in 2019 = b = number of managers left in 2019

Number of employees joined in 2017 = 586 + a – 492 = 94 + a

Number of managers those joined in 2017 = 304 + a – 230 = 74 + a

So, 20% of (94+ a) = 25% of (74 + a)

376 + 4a = 370 + 5a

So, a = 6

So, number of employees joined in 2017 = 94 + 6 = 100

Number of managers joined in 2017 = 74 + 6 = 80

Also, 20% of number of employees joined in 2015 = a = 6

Number of employees joined in 2015 = 6 x 5 = 30

25% of managers joined in 2015 = a = 6

Number of managers joined in 2015 = 6 x 4 = 24

Also, number of employees left in 2015 = 438 + 30 – 434 = 34

Number of managers left in 2011 = 204 + 24 – 210 = 18

20% of number of employees joined in 2013 = 34 (number of employees left in 2015)

Number of employees joined in 2013 = 34 x 5 = 170

25% of managers joined in 2013 = 18

Number of managers joined in 2013 = 18 x 4 = 72

The following table gives number of employees joined each year

Total employees joined in 2017 = 100

Number of managers joined in 2017 = 80

Number of non-managers joined in 2017 = 100 – 80 = 20

Hence answer is option A

Test: Quantitative Aptitude - 2 - Question 8
Save

Directions: Read the following information carefully and answer the questions based on it.

The following bar graph shows the number of employees and number of managers working in a company as on 31st December of different years. The company was started in 2010 and from then 1/5thof the employees and 1/4th of managers who joined the company in any year leave the company after exactly two years and no other employee leaves at any other time.

Total employees in company = Managers + Non – Managers

It is also known that 12 employees left in 2016 and 8managers left in 2014. In 2017 as well as 2019, all the employees who left were managers.

Q. Find number of employees joined in 2014?
Test: Quantitative Aptitude - 2 - Question 9
Save

Directions: Read the following information carefully and answer the questions based on it.

The following bar graph shows the number of employees and number of managers working in a company as on 31st December of different years. The company was started in 2010 and from then 1/5thof the employees and 1/4th of managers who joined the company in any year leave the company after exactly two years and no other employee leaves at any other time.

Total employees in company = Managers + Non – Managers

It is also known that 12 employees left in 2016 and 8managers left in 2014. In 2017 as well as 2019, all the employees who left were managers.

Q. Find number of non-Managers left in 2018?
Detailed Solution for Test: Quantitative Aptitude - 2 - Question 9

It is known that 12 employees left in 2016

Let number of employees joined in 2016 = K

434 + K – 12 = 492

K = 70 (Number of employees joined in 2016

1/5 of number of employees those joined, leaves exactly after two years, so

1/5 of number of employees joined in 2014 = 12

Number of employees joined in 2014 = 12 x 5 = 60

Similarly in 2018 number of employees joined = 612 + 1/5 of 70 – 586 = 40

(70 employees those joined in 2016, 1/5 of them left in 2018)

It is known that 8managers left in 2014

So, number of managers joined in 2014 = 204 + 8 – 164 = 48

25% of managers those joined, leaves exactly after 2 years. So,

25% of managers joined in 2012 = 8

Number of managers joined in 2012 = 4 x 8 = 32

Number of managers joined in 2016 = 230 + 25% of48 –210 = 32

(48managers those joined in 2018, 25% of them left in 2016)

Let the number of employees left in 2017 = a = number of managers left in 2017

Let number of employees left in 2019 = b = number of managers left in 2019

Number of employees joined in 2017 = 586 + a – 492 = 94 + a

Number of managers those joined in 2017 = 304 + a – 230 = 74 + a

So, 20% of (94+ a) = 25% of (74 + a)

376 + 4a = 370 + 5a

So, a = 6

So, number of employees joined in 2017 = 94 + 6 = 100

Number of managers joined in 2017 = 74 + 6 = 80

Also, 20% of number of employees joined in 2015 = a = 6

Number of employees joined in 2015 = 6 x 5 = 30

25% of managers joined in 2015 = a = 6

Number of managers joined in 2015 = 6 x 4 = 24

Also, number of employees left in 2015 = 438 + 30 – 434 = 34

Number of managers left in 2011 = 204 + 24 – 210 = 18

20% of number of employees joined in 2013 = 34 (number of employees left in 2015)

Number of employees joined in 2013 = 34 x 5 = 170

25% of managers joined in 2013 = 18

Number of managers joined in 2013 = 18 x 4 = 72

The following table gives number of employees joined each year

We know that 70 employees joined in 2016

Number of employees left in 2018 = 20% of 70 = 14

Number of managers joined in 2016 = 32

Number of managers left in 2018 = 25% of 32 = 8

So, number of Non managers left in 2018 = 14 – 8 = 6

Hence answer is D

Test: Quantitative Aptitude - 2 - Question 10
Save

Directions: Read the following information carefully and answer the questions based on it.

The following bar graph shows the number of employees and number of managers working in a company as on 31st December of different years. The company was started in 2010 and from then 1/5thof the employees and 1/4th of managers who joined the company in any year leave the company after exactly two years and no other employee leaves at any other time.

Total employees in company = Managers + Non – Managers

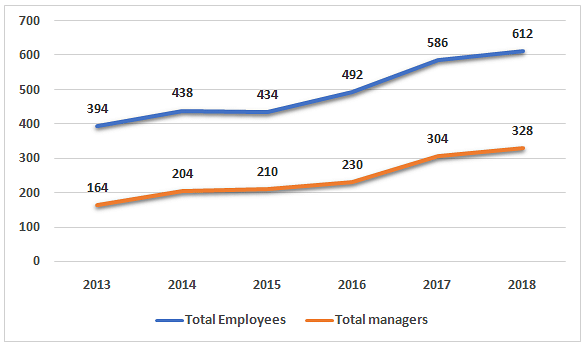
It is also known that 12 employees left in 2016 and 8managers left in 2014. In 2017 as well as 2019, all the employees who left were managers.

Q. Find number of managers left the company from 2014 to 2020?
Detailed Solution for Test: Quantitative Aptitude - 2 - Question 10

It is known that 12 employees left in 2016

Let number of employees joined in 2016 = K

434 + K – 12 = 492

K = 70 (Number of employees joined in 2016

1/5 of number of employees those joined, leaves exactly after two years, so

1/5 of number of employees joined in 2014 = 12

Number of employees joined in 2014 = 12 x 5 = 60

Similarly in 2018 number of employees joined = 612 + 1/5 of 70 – 586 = 40

(70 employees those joined in 2016, 1/5 of them left in 2018)

It is known that 8managers left in 2014

So, number of managers joined in 2014 = 204 + 8 – 164 = 48

25% of managers those joined, leaves exactly after 2 years. So,

25% of managers joined in 2012 = 8

Number of managers joined in 2012 = 4 x 8 = 32

Number of managers joined in 2016 = 230 + 25% of48 –210 = 32

(48managers those joined in 2018, 25% of them left in 2016)

Let the number of employees left in 2017 = a = number of managers left in 2017

Let number of employees left in 2019 = b = number of managers left in 2019

Number of employees joined in 2017 = 586 + a – 492 = 94 + a

Number of managers those joined in 2017 = 304 + a – 230 = 74 + a

So, 20% of (94+ a) = 25% of (74 + a)

376 + 4a = 370 + 5a

So, a = 6

So, number of employees joined in 2017 = 94 + 6 = 100

Number of managers joined in 2017 = 74 + 6 = 80

Also, 20% of number of employees joined in 2015 = a = 6

Number of employees joined in 2015 = 6 x 5 = 30

25% of managers joined in 2015 = a = 6

Number of managers joined in 2015 = 6 x 4 = 24

Also, number of employees left in 2015 = 438 + 30 – 434 = 34

Number of managers left in 2011 = 204 + 24 – 210 = 18

20% of number of employees joined in 2013 = 34 (number of employees left in 2015)

Number of employees joined in 2013 = 34 x 5 = 170

25% of managers joined in 2013 = 18

Number of managers joined in 2013 = 18 x 4 = 72

The following table gives number of employees joined each year

Number of managers left in 2014 = 25% of number of managers joined in 2012

Similarly, we can find for required years

Required number of managers left = 25% of (32 + 72 + 48 + 24 + 32 + 80 + 32) = 80

Hence answer is option B

Test: Quantitative Aptitude - 2 - Question 11
Save

Directions: Read the following information carefully and answer the questions based on it.

Equation 1. 6P2 – 19P – (M2 – 4) = 0, M is positive integer

Equation 2. 4(Z – 4Y)2 + 4Y2 + K2 – 4YK = 0

(-7/3) and K is the root of equation 1.

Q. Find the value of (Z + Y)?
Detailed Solution for Test: Quantitative Aptitude - 2 - Question 11

Equation 1.

6P2 – 19P – (M2 – 4) = 0

6 x (-7/3)2 – 19 x (-7/3) = (M2 – 4)

M2 = 77 + 4

Value of M = 9

So,

(-7/3) + K = 19/6

Value of K = 11/2

Equation 2.

4(Z – 4Y)2 + 4Y2 + K2 – 4YK = 0

(Z – 4Y)2 + Y2 + K2/4 – YK = 0

(Z – 4Y)2 + (Y – K/2)2 = 0

Z = 4Y, Y = K/2

Value of Y = 11/4

Z = 4 x 11/4 = 11

According to question,

Required value = (Z + Y) = 11 + 11/4 = 55/4 = 13.75

Hence answer is option D

Test: Quantitative Aptitude - 2 - Question 12
Save

Directions: Read the following information carefully and answer the questions based on it.

There are six friends planning a trip to Manali, all resides in same Hostel somewhere in Delhi. On Monday at 6.30 am, they all started from their hostel, by their own individual cars.

  • Speed of P is 50% more than that of R, and Q is 48 km behind Manali when T reached Manali.
  • S covered the whole distance in 56 minutes more than the person who was the first to reached Manali.
  • T covered half of the journey with speed of K km/h, half of remaining with speed of (K + 5) km/h and rest distance with speed of (K + 20) km/h.
  • R covered 60% of whole journey in 3 hours 36 minutes, while initial speed of T is 32 km/h less than S. U was the first person to reached Manali, which covered whole journey with speed of 100 km/h
  • M2 – 64M + 768 = 0

Where distance between Hostel and Manali is 5 times of larger root of given equation.

Q. Who was the second person to reached Manali?
Detailed Solution for Test: Quantitative Aptitude - 2 - Question 12

First, we need to calculate the distance between Hostel and Manali.

M2 – 64M + 768 = 0

(M – 48) (M – 16) = 0

M = 16, 48

Total distance between Hostel and Manali = 48 x 5 = 240 km

Time taken by U to reached Manali = 240/100 = 2 hours 24 minutes

Time taken by S to reached Manali = 2 hours 24 minutes + 56 minutes = 3 hours 20 minutes = 10/3 hours

Speed of S for whole journey = 240 / (10/3) = 72 km/h

Initial speed of T = 72 – 32 = 40 km/h

Time taken by T to reached Manali = 120 / 40 + 60/45 + 60/60 = 5 hours 20 minutes = 16/3 hours

In 16/3 hours, distance travelled by Q = 240 – 48 = 192 km

So, total distance traveled by Q in = (16/3) x (240/192) = 6 hours 40 minutes = 20/3 hours

Speed of Q for whole journey = 240 / (20/3) = 36 km/h

R covers 60% of total distance in 3 hours 36 minutes

So, time taken by R to cover whole distance = 18/5 x 5/3 = 6 hours

So, time taken by P to cover whole distance = 2/3 x 6 = 4 hours

Speed of P = 240/4 = 60 km/h

Speed of R = 240/6 = 40 km/h

According to questions,

Second person to reached Manali = S

Hence answer is option B

Test: Quantitative Aptitude - 2 - Question 13
Save

Directions: Read the following information carefully and answer the questions based on it.

There are six friends planning a trip to Manali, all resides in same Hostel somewhere in Delhi. On Monday at 6.30 am, they all started from their hostel, by their own individual cars.

  • Speed of P is 50% more than that of R, and Q is 48 km behind Manali when T reached Manali.
  • S covered the whole distance in 56 minutes more than the person who was the first to reached Manali.
  • T covered half of the journey with speed of K km/h, half of remaining with speed of (K + 5) km/h and rest distance with speed of (K + 20) km/h.
  • R covered 60% of whole journey in 3 hours 36 minutes, while initial speed of T is 32 km/h less than S. U was the first person to reached Manali, which covered whole journey with speed of 100 km/h
  • M2 – 64M + 768 = 0

Where distance between Hostel and Manali is 5 times of larger root of given equation.

Q. What will be the time when the last person will reach Manali?
Detailed Solution for Test: Quantitative Aptitude - 2 - Question 13

First, we need to calculate the distance between Hostel and Manali.

M2 – 64M + 768 = 0

(M – 48) (M – 16) = 0

M = 16, 48

Total distance between Hostel and Manali = 48 x 5 = 240 km

Time taken by U to reached Manali = 240/100 = 2 hours 24 minutes

Time taken by S to reached Manali = 2 hours 24 minutes + 56 minutes = 3 hours 20 minutes = 10/3 hours

Speed of S for whole journey = 240 / (10/3) = 72 km/h

Initial speed of T = 72 – 32 = 40 km/h

Time taken by T to reached Manali = 120 / 40 + 60/45 + 60/60 = 5 hours 20 minutes = 16/3 hours

In 16/3 hours, distance travelled by Q = 240 – 48 = 192 km

So, total distance traveled by Q in = (16/3) x (240/192) = 6 hours 40 minutes = 20/3 hours

Speed of Q for whole journey = 240 / (20/3) = 36 km/h

R covers 60% of total distance in 3 hours 36 minutes

So, time taken by R to cover whole distance = 18/5 x 5/3 = 6 hours

So, time taken by P to cover whole distance = 2/3 x 6 = 4 hours

Speed of P = 240/4 = 60 km/h

Speed of R = 240/6 = 40 km/h

Q is the last person to reached Manali, in = 6 hours 40 minutes

Required time = 6:30 am + 6 hours + 40 minutes = 1:10 Pm

Hence answer is option E

Test: Quantitative Aptitude - 2 - Question 14
Save

Directions: Read the following information carefully and answer the questions based on it.

There are six friends planning a trip to Manali, all resides in same Hostel somewhere in Delhi. On Monday at 6.30 am, they all started from their hostel, by their own individual cars.

  • Speed of P is 50% more than that of R, and Q is 48 km behind Manali when T reached Manali.
  • S covered the whole distance in 56 minutes more than the person who was the first to reached Manali.
  • T covered half of the journey with speed of K km/h, half of remaining with speed of (K + 5) km/h and rest distance with speed of (K + 20) km/h.
  • R covered 60% of whole journey in 3 hours 36 minutes, while initial speed of T is 32 km/h less than S. U was the first person to reached Manali, which covered whole journey with speed of 100 km/h
  • M2 – 64M + 768 = 0

Where distance between Hostel and Manali is 5 times of larger root of given equation.

Q. If a person who was second last to reached Manali, travel with his original speed for the time in which person who secured rank 2 reached Manali, then find what % of whole journey he covered?
Detailed Solution for Test: Quantitative Aptitude - 2 - Question 14

First, we need to calculate the distance between Hostel and Manali.

M2 – 64M + 768 = 0

(M – 48) (M – 16) = 0

M = 16, 48

Total distance between Hostel and Manali = 48 x 5 = 240 km

Time taken by U to reached Manali = 240/100 = 2 hours 24 minutes

Time taken by S to reached Manali = 2 hours 24 minutes + 56 minutes = 3 hours 20 minutes = 10/3 hours

Speed of S for whole journey = 240 / (10/3) = 72 km/h

Initial speed of T = 72 – 32 = 40 km/h

Time taken by T to reached Manali = 120 / 40 + 60/45 + 60/60 = 5 hours 20 minutes = 16/3 hours

In 16/3 hours, distance travelled by Q = 240 – 48 = 192 km

So, total distance traveled by Q in = (16/3) x (240/192) = 6 hours 40 minutes = 20/3 hours

Speed of Q for whole journey = 240 / (20/3) = 36 km/h

R covers 60% of total distance in 3 hours 36 minutes

So, time taken by R to cover whole distance = 18/5 x 5/3 = 6 hours

So, time taken by P to cover whole distance = 2/3 x 6 = 4 hours

Speed of P = 240/4 = 60 km/h

Speed of R = 240/6 = 40 km/h

Speed of R (Rank 5) = 40 km/h

Travelling time of S (Rank 2) = 10/3 hours

Required % = [(40 x 10) / (240 x 3)] x 100 = 55.55%

Hence answer is option C

Test: Quantitative Aptitude - 2 - Question 15
Save

Directions: Read the following information carefully and answer the questions based on it.

There are six friends planning a trip to Manali, all resides in same Hostel somewhere in Delhi. On Monday at 6.30 am, they all started from their hostel, by their own individual cars.

  • Speed of P is 50% more than that of R, and Q is 48 km behind Manali when T reached Manali.
  • S covered the whole distance in 56 minutes more than the person who was the first to reached Manali.
  • T covered half of the journey with speed of K km/h, half of remaining with speed of (K + 5) km/h and rest distance with speed of (K + 20) km/h.
  • R covered 60% of whole journey in 3 hours 36 minutes, while initial speed of T is 32 km/h less than S. U was the first person to reached Manali, which covered whole journey with speed of 100 km/h
  • M2 – 64M + 768 = 0

Where distance between Hostel and Manali is 5 times of larger root of given equation.

Q. If P takes rest of 5 minutes after travel of every 45 km, then find the time taken by P is how much more or less than time taken by a person who reached Manali 4th. 
Detailed Solution for Test: Quantitative Aptitude - 2 - Question 15

First, we need to calculate the distance between Hostel and Manali.

M2 – 64M + 768 = 0

(M – 48) (M – 16) = 0

M = 16, 48

Total distance between Hostel and Manali = 48 x 5 = 240 km

Time taken by U to reached Manali = 240/100 = 2 hours 24 minutes

Time taken by S to reached Manali = 2 hours 24 minutes + 56 minutes = 3 hours 20 minutes = 10/3 hours

Speed of S for whole journey = 240 / (10/3) = 72 km/h

Initial speed of T = 72 – 32 = 40 km/h

Time taken by T to reached Manali = 120 / 40 + 60/45 + 60/60 = 5 hours 20 minutes = 16/3 hours

In 16/3 hours, distance travelled by Q = 240 – 48 = 192 km

So, total distance traveled by Q in = (16/3) x (240/192) = 6 hours 40 minutes = 20/3 hours

Speed of Q for whole journey = 240 / (20/3) = 36 km/h

R covers 60% of total distance in 3 hours 36 minutes

So, time taken by R to cover whole distance = 18/5 x 5/3 = 6 hours

So, time taken by P to cover whole distance = 2/3 x 6 = 4 hours

Speed of P = 240/4 = 60 km/h

Speed of R = 240/6 = 40 km/h

Speed of P = 60 km/h

Time taken to travel 45 km = 45/60 = 45 minutes

After that he takes rest of 5 minutes.

So, in 50 minutes he travel = 45 km

In 250 minutes = 225 km

Time taken by P to travel whole distance = 250 minutes + 15/60 x 60 = 265 minutes = 4 hours 25 minutes

T secured 4th rank = 5 hours 20 hours

Required difference = 5 hours 20 minutes – 4 hours 25 minutes = 55 minutes

Hence answer is option D

Test: Quantitative Aptitude - 2 - Question 16
Save

Find out the wrong number in the following number series.

5, 9, 25, 61, 125, 230
Detailed Solution for Test: Quantitative Aptitude - 2 - Question 16

5 + 22 = 9

9 + 42 = 25

25 + 62 = 61

61 + 82 = 125

125 + 102 = 225 (not 230)

Test: Quantitative Aptitude - 2 - Question 17
Save

Find out the wrong number in the following number series.

80, 40, 20, 10, 2, 2.5
Detailed Solution for Test: Quantitative Aptitude - 2 - Question 17

80 ÷ 2 = 40

40 ÷ 2 = 20

20 ÷ 2 = 10

10 ÷ 2 = 5 (not 2)

5 ÷ 2 = 2.5

Test: Quantitative Aptitude - 2 - Question 18
Save

Find out the wrong number in the following number series.

50, 60, 80, 110, 180, 200
Detailed Solution for Test: Quantitative Aptitude - 2 - Question 18

50 + 10 x 1 = 60

60 + 10 x 2 = 80

80 + 10 x 3 = 110

110 + 10 x 4 = 150 (not 180)

150 + 10 x 5 = 200

Test: Quantitative Aptitude - 2 - Question 19
Save

Find out the wrong number in the following number series.

1, 5, 40, 210, 1680, 15120
Detailed Solution for Test: Quantitative Aptitude - 2 - Question 19

1 x 5 = 5

5 x 6 = 30 (not 40)

30 x 7 = 210

210 x 8 = 1680

1680 x 9 = 15120

Test: Quantitative Aptitude - 2 - Question 20
Save

Find out the wrong number in the following number series.

100, 40, 200, 40, 400, 80
Detailed Solution for Test: Quantitative Aptitude - 2 - Question 20

100 ÷ 5 = 20 (not 40)

20 x 10 = 200

200 ÷ 5 = 40

40 x 10 = 400

400 ÷ 5 = 80

Information about Test: Quantitative Aptitude - 2 Page
In this test you can find the Exam questions for Test: Quantitative Aptitude - 2 solved & explained in the simplest way possible. Besides giving Questions and answers for Test: Quantitative Aptitude - 2, EduRev gives you an ample number of Online tests for practice

Top Courses for Bank Exams

Download as PDF

Top Courses for Bank Exams

Important Questions for Quantitative Aptitude - 2

Find all the important questions for Quantitative Aptitude - 2 at EduRev.Get fully prepared for Quantitative Aptitude - 2 with EduRev's comprehensive question bank and test resources. Our platform offers a diverse range of question papers covering various topics within the Quantitative Aptitude - 2 syllabus. Whether you need to review specific subjects or assess your overall readiness, EduRev has you covered. The questions are designed to challenge you and help you gain confidence in tackling the actual exam. Maximize your chances of success by utilizing EduRev's extensive collection of Quantitative Aptitude - 2 resources.

Quantitative Aptitude - 2 MCQs with Answers

Prepare for the Quantitative Aptitude - 2 within the Bank Exams exam with comprehensive MCQs and answers at EduRev. Our platform offers a wide range of practice papers, question papers, and mock tests to familiarize you with the exam pattern and syllabus. Access the best books, study materials, and notes curated by toppers to enhance your preparation. Stay updated with the exam date and receive expert preparation tips and paper analysis. Visit EduRev's official website today and access a wealth of videos and coaching resources to excel in your exam.

Online Tests for Quantitative Aptitude - 2

Practice with a wide array of question papers that follow the exam pattern and syllabus. Our platform offers a user-friendly interface, allowing you to track your progress and identify areas for improvement. Access detailed solutions and explanations for each test to enhance your understanding of concepts. With EduRev's Online Tests, you can build confidence, boost your performance, and ace Quantitative Aptitude - 2 with ease. Join thousands of successful students who have benefited from our trusted online resources.
© EduRev
Education Revolution
Signup to see your scores go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup