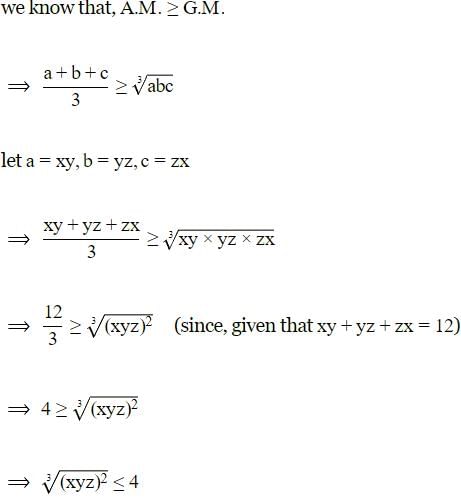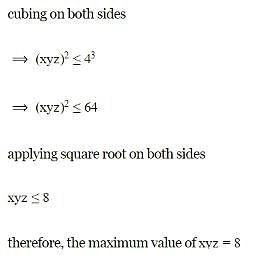GMAT Classic Mock Test - 1 - GMAT MCQ
30 Questions MCQ Test - GMAT Classic Mock Test - 1
The maximum recommended pulse rate R, when exercising, for a person who is x years of age is given by the equation R = 176 - 0.8x. What is the age, in years, of a person whose maximum recommended pulse rate when exercising is 140?
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
If the average (arithmetic mean) of 5 numbers j, j + 5, 2j - 1, 4j -2, and 5j- 1 is 8, what is the value of j?
Guadalupe owns 2 rectangular tracts of land. One is 300 m by 500 m and the other is 250 m by 630 m. The combined area of these 2 tracts is how many square meters?
There are five sales agents in a certain real estate office. One month Andy sold twice as many properties as Ellen, Bob sold 3 more than Ellen, Cary sold twice as many as Bob, and Dora sold as many as Bob and Ellen together. Who sold the most properties that month?
In a field day at a school, each child who competed in n events and scored a total of ρ points was given an overall score of (ρ/n) + n. Andrew competed in 1 event and scored 9 points. Jason competed in 3 events and scored 5, 6, and 7 points, respectively. What was the ratio of Andrew's overall score to Jason's overall score?
A certain work plan for September requires that a work team, working every day, produce an average of 200 items per day. For the first half of the month, the team produced an average of 150 items per day. How many items per day must the team average during the second half of the month ifitis to attain the average daily production rate required by the work plan?
A souvenir vendor purchased 1,000 shirts for a special event at a price of $5 each. The vendor sold 600 of the shirts on the day of the event for $12 each and 300 of the shirts in the week following the event for $4 each. The vendor was unable to sell the remaining shirts. What was the vendor's gross profit on the sale of these shirts?
If xy+yz+zx=12, where x,y,z are positive values, then the greatest value of xyz is
To order certain plants from a catalog, it costs $3.00 per plant, plus a 5 percent sales tax, plus $6.95 for shipping and handling regardless of the number of plants ordered. If Company C ordered these plants from the catalog at the total cost of $69.95, how many plants did Company C order?
The value of Maureen's investment portfolio has decreased by 5.8 percent since herinitial investment in the portfolio. If her initial investment was $16,800, what is the current value of the portfolio?
The value of Maureen's investment portfolio hasdecreased by 5.8 percent since herinitial investment in the portfolio. If her initial investment was $16,800, what is the current value of the portfolio?
Company C produces toy trucks at a cost of $5.00 each for the first 100 trucks and $3.50 for each additional truck. If 500 toy trucks were produced by Company C and sold for $10.00 each, what was Company C's gross profit?
A group of store managers must assemble 280 displays for an upcoming sale. If they assemble 25 percent of the displays during the first hour and 40 percent of the remaining displays during the second hour, how many of the displays will not have been assembled by the end of the second hour?
The annual profit or loss for the three divisions of Company T for the years 1991 through 1995 are summarized in the table shown, where losses are enclosed in parentheses. For which division and which three consecutive years shown was the division’s profit or loss for the three-year period closest to $0 ?

How many members of the staff of Advanced Computer Technology Consulting are women from outside the United States?
- one-fourth of the staff at Advanced Computer Technology Consulting are men
- 20% of the staff, or 20 individuals, are men from the U.S.; there are twice as many women from the U.S. as men from the U.S.
In a certain class, a teacher distributed a few candies and a few bars among the students such that each student got an equal number of candies and an equal number of bars and no candies or bars remained undistributed. How many students were there in the class?
(1) The teacher distributed 180 candies and 40 bars.
(2) The total number of items received by each student was less than or equal 20.
If no bulk purchase discount applies, what is the price of 13 oranges and 12 apples?
(1) The price of 39 oranges and 36 apples is $111.
(2) The price of 3 oranges and 2 apples is $7.
What is the price of an orange?
(1) The price of 3 oranges and 2 apples is $7.
(2) The price of an orange and the price of an apple are both integers.
A trader purchased three products - Product X, Product Y, and Product Z - for a sum of $500,000. Did the trader pay more than $200,000 for Product Z?
(1) The sum the trader paid for Product X and Product Y combined was 3 times the sum the trader paid for Product X.
(2) The trader paid more to purchase Product Z than to purchase Product Y.
A teacher distributed pens, pencils, and erasers among the students of his class, such that all students got an equal number of pens, an equal number of pencils, and an equal number of erasers. If no pens, pencils, or erasers remained with the teacher, how many students were in the class?
(1) Each student got pens, pencils, and erasers in the ratio 3:4:5, respectively.
(2) The teacher distributed a total of 27 pens, 36 pencils, and 45 erasers.
If neither x nor y is equal to 0, is 3x − 2y = 0?
(1) 27x3 − 8y3 = 0
(2) 9x2 − 4y2 = 0
Did David solve more questions than Steve in a 2-hour test?
(1) Thrice the number of questions that David solved in the test was greater than 6 less than thrice the number of questions that Steve solved in the test.
(2) Twice the number of questions that David solved in the test was greater than 4 less than twice the number of questions that Steve solved in the test.
Each of the 25 books on bookshelf X is thinner than each of the 25 books on bookshelf Y. Is the median thickness of the 50 books less than 20-millimeters?
(1) The thinnest book on bookshelf X is 2 millimeters thick.
(2) The thinnest book on bookshelf Y is 20 millimeters thick.
A box has at least one ball of each of the colors red, green, and blue and no balls of any other color. If one ball is drawn randomly from the box, is the probability that the drawn ball is red same as the probability that the drawn ball is blue but NOT the same as the probability that the drawn ball is green?
(1) There are 5 balls in the box.
(2) The number of green balls is greater than the number of blue balls.
For all integers n, the function f is defined by f(n) = (a)6/n, where a is a constant. What is the value of f(1)?
(1) f(2) = 64
(2) f(3) = 16
If t and x are integers, what is the value of x?
(1) x2 / t2 = 4 / 9
(2) x > 0 and t > 0
The cost of a certain phone call was $0.75 for the first 3 minutes and $0.20 for each additional minute after the first 3 minutes. Did the phone call last longer than 15 minutes?
(1) The cost of the phone call was less than $4.16
(2) The cost of the phone call was greater than $3.35
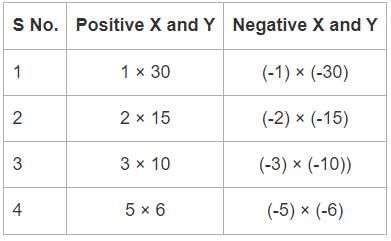
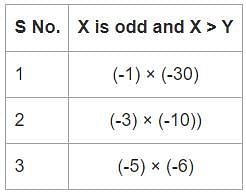
What is the value of X, if X and Y are two distinct integers and their product is 30?
(1) X is an odd integer
(2) X > Y
What is the standard deviation (SD) of the four numbers p, q, r, and s?
(1) The sum of p, q, r, and s is 24.
(2) The sum of the squares of p, q, r, and s is 224.