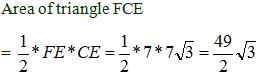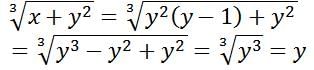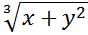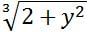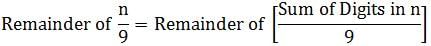GMAT Classic Mock Test - 4 - GMAT MCQ
30 Questions MCQ Test - GMAT Classic Mock Test - 4
There are 5,280 feet in 1 mile and 12 inches in one foot. How many inches are in a mile?
5n + 2 > 12 and 7n - 5 < 44; n must be between which numbers?
During the course of an hour, an employee at Ultimate Packing Solutions wrapped packages weighing 48, 32, 62, 12, 40, and 8 pounds. What was the median weight of the packages that the employee packed?
A yellow taxi cab went from Downtown to the Beachside and back at an average speed of 2/3 miles per hour. If the distance from Beachside to Downtown is 1 mile, and the trip back took half as much time as the trip there, what was the average speed of the yellow taxi cab on the way to Beachside?
Assume that x and y are positive integers such that (x/y) > 1. Which of the following must be less than 1?
A group of 5 investment bankers and 5 clients recently frequented the Fine Tiger Indian Restaurant. The total bill for the meal, including 20% gratuity, came to $960. On average, how much did the meal of each individual cost before gratuity?
In a local intramural basketball league, there are 10 teams and each team plays every other team exactly one time. Assuming that each game is played by only two teams, how many games are played in total?
Peter's bank account has p dollars. John's bank account has 5 times what Peter's bank account has and 1/3 what Fred's bank account has. How much more is in Fred's bank account than is in Peter's bank account, in terms of p?
A computer store offers employees a 20% discount off the retail price. If the store purchased a computer from the manufacturer for $1000 dollars and marked up the price 20% to the final retail price, how much would an employee save if he purchased the computer at the employee discount (20% off retail price) as opposed to the final retail price.
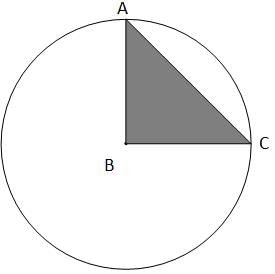
If points A and C both lie on the circle with center B and the measurement of angle ABC is not a multiple of 30, what is the ratio of the area of the circle centered at point B to the area of triangle ABC?
A fair sided die labeled 1 to 6 is tossed three times. What is the probability the sum of the 3 throws is 16?
A project manager needs to select a group of 4 people from a total of 4 men and 4 women. How many possible group combinations exist such that no group has all men or all women?
Walking across campus, a student interviewed a group of students. 25% of the students took a finance class last semester, 50% took a marketing class last semester, and 40% took neither a finance nor a marketing class last semester. What percent of the students in the group took both a finance and a marketing class?
The ratio of a compound, by weight, consisting only of substances x, y, and z is 4:6:10, respectively. Due to a dramatic increase in the surrounding temperature, the composition of the compound is changed such that the ratio of x to y is halved and the ratio of x to z is tripled. In the changed compound, if the total weight is 58 lbs, how much does substance x weigh?
Directions: Each GMAT Data Sufficiency problem consists of a question and two statements labeled (1) and (2), that provide data. Based on the data given plus your knowledge of mathematics and everyday facts, you must decide whether the data are sufficient for answering the question. The five answer choices are the same for every data sufficiency question.
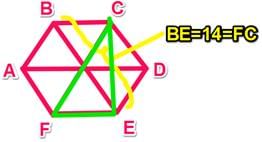
What is the area of a triangle (with vertices at FCE) that is inscribed in a hexagon with vertices at ABCDE?
(1) The hexagon is regular and BE = 14.
(2) EC = 7√3.
Directions: Each GMAT Data Sufficiency problem consists of a question and two statements labeled (1) and (2), that provide data. Based on the data given plus your knowledge of mathematics and everyday facts, you must decide whether the data are sufficient for answering the question. The five answer choices are the same for every data sufficiency question.
How many integers are there between m and n, exclusive, if m and n are themselves integers?
(1) m − n = 8
(2) There are 5 integers between, but not including, m − 1 and n − 1.
Directions: Each GMAT Data Sufficiency problem consists of a question and two statements labeled (1) and (2), that provide data. Based on the data given plus your knowledge of mathematics and everyday facts, you must decide whether the data are sufficient for answering the question. The five answer choices are the same for every data sufficiency question.
For integers w, x, y, and z, is wxyz = -1?
(1) wx / yz = -1
(2) w = -1/x and y = 1/z
Directions: Each GMAT Data Sufficiency problem consists of a question and two statements labeled (1) and (2), that provide data. Based on the data given plus your knowledge of mathematics and everyday facts, you must decide whether the data are sufficient for answering the question. The five answer choices are the same for every data sufficiency question.
If the product of j and k does not equal zero, is j<0 and k>0?
(1) (-j, k) lies above the x-axis and to the right of the y-axis.
(2) (j, -k) lies below the x-axis and to the left of the y-axis.
What is the average (arithmetic mean) of w, x, y, z, and 10?
1. the average (arithmetic mean) of w and y is 7.5; the average (arithmetic mean) of x and z is 2.5
2. -[-z - y -x - w] = 20
Is 13N a positive number?
1. -21N is a negative number
2. N2 < 1
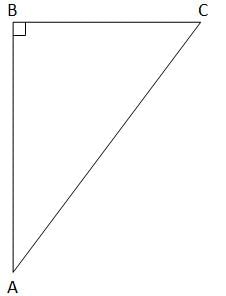
In triangle ABC, what is the measurement of angle C?
1. The sum of the measurement of angles A and C is 120
2. The sum of the measurement of angles A and B is 80
ohn is trying to get from point A to point C, which is 15 miles away directly to the northeast; however the direct road from A to C is blocked and John must take a detour. John must travel due north to point B and then drive due east to point C. How many more miles will John travel due to the detour than if he had traveled the direct 15 mile route from A to C?
1. Tha ratio of the distance going north to the distance going east is 4 to 3
2. The distance traveled north going the direct route is 12
If the product of X and Y is a positive number, is the sum of X and Y a negative number?
1. X > Y5
2. X > Y6
If x is a positive integer, is x divided by 5 an odd integer?
1. x contains only odd factors
2. x is a multiple of 5
Is (2y+z)(3x)(5y)(7z) < (90y)(14z)?
1. y and z are positive integers; x = 1
2. x and z are positive integers; y = 1
If x is not zero, is x2 + 2x > x2 + x?
1. xodd integer > xeven integer
2. x2 + x - 12 = 0
If x and y are positive integers, is the following cube root an integer?
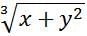
If w, x, y, and z are the digits of the four-digit number N, a positive integer, what is the remainder when N is divided by 9?
1. w + x + y + z = 13
2. N + 5 is divisible by 9
If x and y are distinct positive integers, what is the value of x4 - y4?
1. (y2 + x2)(y + x)(x - y) = 240
2. xy = yx and x > y