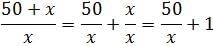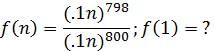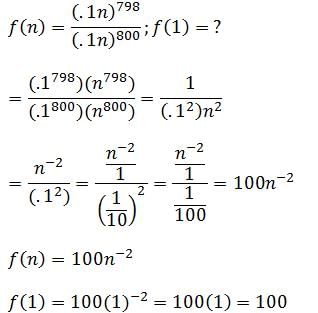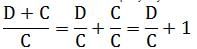GMAT Classic Mock Test - 5 - GMAT MCQ
30 Questions MCQ Test - GMAT Classic Mock Test - 5
If n # z = n2 - nz - 2(z-2)n for integers n and z, what is the value of 2 # 2?
If circles x and y have the same area and circle x has a circumference of 16π, half of the radius of circle y is:
For which of the following values of x is the fraction below an integer:
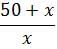
A computer store offers employees a 20% discount off the retail price. If the store purchased a computer from the manufacturer for $1000 dollars and marked up the price 20% to the final retail price, how much would an employee save if he purchased the computer at the employee discount (20% off retail price) as opposed to the final retail price.
K is the set of positive integers less than 40 that are also divisible by 2. M is the set of the square roots of K. How many integers are in the set M?
There are 4 more women than there are men on a local co-ed softball team. If there are a total of 16 players on the team, what is the ratio of men to women?
In a recent head-to-head run-off election, 12,000 absentee ballets were cast. 1/3 of the absentee ballets were thrown out and 1/4 of the remaining absentee ballets were cast for Candidate A. How many absentee votes did Candidate B receive?
In May, the grounds keeper at Spring Lake Golf Club built a circular green with an area of 100π square feet. In August, he doubled the distance from the center of the green to the edge of the green. What is the total area of the renovated green?
In baseball, the batting average is defined as the ratio of a player’s hits to at bats. If a player had anywhere from 4 to 6 at bats in a recent game and had anywhere from 2 to 3 hits in the same game, the player’s actual batting average for that game could fall anywhere between
Let f(x) = x2 + bx + c. If f(1) = 0 and f(-4) = 0, then f(x) crosses the y-axis at what y-coordinate?
What fraction of seven lettered words formed using the letters of the words CLASSIC will have the two C's always together?
Mariah has decided to hire three workers. To determine whom she will hire, she has selected a group of 10 candidates. She plans to have one working interview with 3 of the 10 candidates every day to see how well they work together. How many days will it take her to have working interviews with all the different combinations of job candidates?
x is a positive integer; what is the value of x?
(1) The sum of any two positive factors of x is even
(2) x is a prime number and x < 4
x is an integer and x raised to any odd integer is greater than zero; is w - z greater than 5 times the quantity 7x-1 - 5x?
(1) z < 25 and w = 7x
(2) x = 4
x is a positive integer greater than two; is (x3 + 19837)(x2 + 5)(x – 3) an odd number?
(1) the sum of any prime factor of x and x is even
(2) 3x is an even number
If N, C, and D are positive integers, what is the remainder when D is divided by C?
(1) If D+1 is divided by C+1, the remainder is 5.
(2) If ND+NC is divided by CN, the remainder is 5.
What is the value of x?
(1) The average (arithmetic mean) of 5, x2, 2, 10x, and 3 is -3.
(2) The median of 109, -32, -30, 208, -15, x, 10, -43, 7 is -5.
How many prime numbers are there between the integers 7 and X, not-inclusive?
(1) 15 < X < 34
(2) X is a multiple of 11 whose sum of digits is between 1 and 7
As a result of dramatic changes in the global currency market, the value of every item in Country X plummeted by 50% from 1990 to 1995. What was the value of a copy of St. Augustine's Confessions in Country X's currency in 1990? (Assume that the only variable influencing changes in the value of the book is the value of Country X's currency.)
(1) The value of St. Augustine's Confessions at the end of 1993 was $30
(2) If the value of every item in Country X had plummeted by 50% from 1995 to 2000, the value of St. Augustine's Confessions in 2000 would have been $25
If 10x + 10y + 16x2 + 25y2 = 10 + Z, what is the value of x + y?
(1) Z = (4x)2 + (5y)2
(2) x = 1
If X is a positive integer, is X divisible by 4?
(1) X has at least two 2s in its prime factorization
(2) X is divisible by 2
n is a positive number; z – 15 is also a positive number; is z/n less than one?
(1) z – n > 0
(2) n < 15
Is (-x) a negative number?
(1) 4x2 – 8x > (2x)2 – 7x
(2) x + 2 > 0
If A and B are integers, is B > A?
(1) B > 10
(2) A < 10
What is the value of xn – ny – nz?
(1) x – y – z = 10
(2) n = 5
X and Y are both positive integers whose combined factors include 3 and 7. Is the sum X + Y + 1 an odd integer?
(1) Both X and Y are divisible by 2
(2) X + 2 = Y