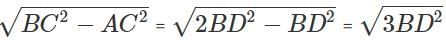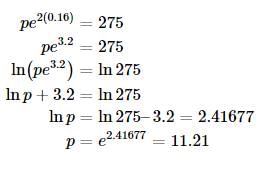GMAT Classic Mock Test - 8 - GMAT MCQ
30 Questions MCQ Test - GMAT Classic Mock Test - 8
Three positive integers a, b, and c are such that their average is 20 and a ≤ b ≤ c. If the median is (a + 11), what is the least possible value of c?
How many four-digit positive integers exist that contain the block 25 and are divisible by 75. (2250 and 2025 are two such numbers)?
A movie hall sold tickets to one of its shows in two denominations, $11 and $7. A fourth of all those who bought a ticket also spent $4 each on refreshments at the movie hall. If the total collections from tickets and refreshments for the show was $124, how many $7 tickets were sold? Note: The number of $11 tickets sold is different from the number of $7 tickets sold.
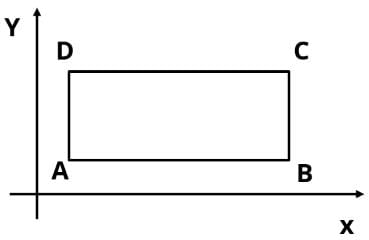
Rectangle ABCD is constructed in the xy-plane so that sides AB and CD are parallel to the x-axis. Both the x and y coordinates of all four vertices of the rectangle are integers. How many rectangles can be constructed if x and y coordinates satisfy the inequality 11 < x < 29 and 5 ≤ y ≤ 13?
Susan invited 13 of her friends for her birthday party and created return gift hampers comprising one each of $3, $4, and $5 gift certificates. One of her friends did not turn up and Susan decided to rework her gift hampers such that each of the 12 friends who turned up got $13 worth gift certificates. How many gift hampers did not contain $5 gift certificates in the new configuration?
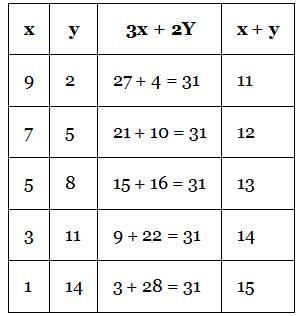
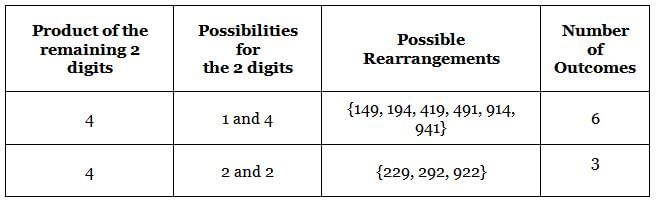
149 is a 3-digit positive integer, product of whose digits is 1 × 4 × 9 = 36. How many 3-digit positive integers exist, product of whose digits is 36?
A student is required to solve 6 out of the 10 questions in a test. The questions are divided into two sections of 5 questions each. In how many ways can the student select the questions to solve if not more than 4 questions can be chosen from either section?
How many 6-digit numbers can be formed using the digits {1, 2, 3, ... 9} such that any digit that appears in such a number appears at least twice?
If y is the highest power of a number 'x' that can divide 101! without leaving a remainder, then for which among the following values of x will y be the highest?
If a, b, .. , j are real numbers such that (a - 1)2 + (b - 2)4 + (c - 3)6 + ... + (j - 10)20 = 0, what is the value of b × d × f × h × j ?
What is the sum of all 3-digit positive integers such that all the digits of each of the number is even?
What is the least number that when divided by 44 leaves a remainder 31, when divided by 56 leaves a remainder 43, and when divided by 32 leaves a remainder 19?
What is the product of all the factors of the cube of a positive integer 'n' if the product of all the factors of square of n is n3?
How many even 3-digit positive integers exist whose digits are distinct?
If x and y are non-negative integers such that 4x + 7y = 68, how many values are possible for (x + y)?
Is x|x| = x2?
Statement 1: x(1 – x2) < 0
Statement 2: x(1 – x) < 0
What is the range of 5 distinct single digit positive integers if their average is 5?
Statement 1: Their median is 6.
Statement 2: The average of the 3 largest among the 5 numbers is 7.
What is the range of 3 positive integers a, b, and c?
Statement 1: 21a = 9b = 7c
Statement 2: a + 8, b, and c, in that order are in AP.
Is the twelve-digit positive integer a perfect square?
Statement 1: The number comprises only the digits 0, 1, and 2, each written four times.
Statement 2: The sum of the digits of the twelve-digit number is 12.
If a and b are positive integers, is (a + b) prime?
Statement 1: 13a = 43b
Statement 2: 8a = 15b
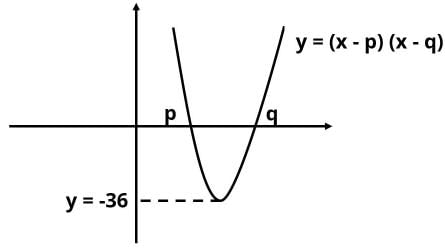
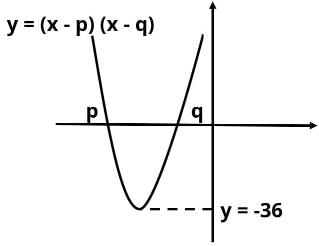
If y = (x - p)(x - q), is the sum of integers p and q positive?
Statement 1: The curve cuts the y-axis at -20.
Statement 2: Minimum value of y is -36.
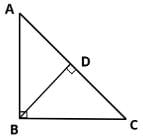
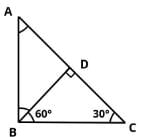
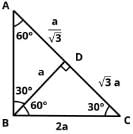
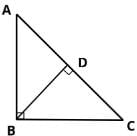
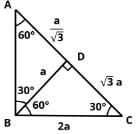
In right triangle ABC, what is the ratio in which point D divides the hypotenuse AC? BD is perpendicular to AC.
Statement 1: BC = 2BD
Statement 2: AC = 2AB
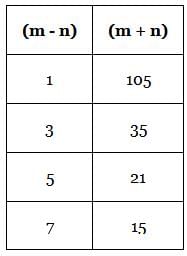
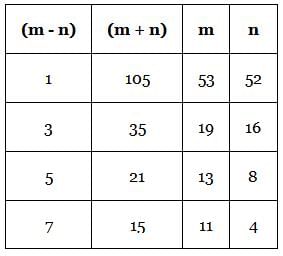
What is the value of (m + n) if m and n are positive integers?
Statement 1: m2 – n2 = 105
Statement 2: Neither m nor n is divisible by 8.
If sets A and B have n elements each, are the ranges of the two sets equal?
Statement 1: Both sets are symmetric about their respective means.
Statement 2: The median of both the sets is 50.
If a, b, and c are non-zero numbers, how many of these three numbers are positive numbers?
Statement 1: a + b + c > 0
Statement 2: The number of negative numbers is more than the number of positive numbers among these three numbers.
Is ‘x’ even?
Statement 1: x3 / 2 is even.
Statement 2: 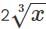 is even.
is even.
When integer y is divided by 2, is the remainder 1?
(1) (−1)(y+2) = −1
(2) y is prime.
Chiku received a $3.50 per hour raise this week. If last week she worked 40 hours per week at her old pay rate, how many fewer hours can she work this week and still guarantee that she makes more this week than she did last week?
(1) She made $620 last week.
(2) Her raise was 20 percent greater than that of any of her coworkers.
If the number of rabbits at a certain pet store is 250 percent greater than the number of hamsters at the same store, how many hamsters are in the store?
(1) There are 40 rabbits in the store.
(2) There are 56 hamsters and rabbits in the store.
The amount of bacteria in a culture after some t hours is given by the function f(t) = pekt where p is a constant. What is the number of bacteria after 8 hours?
(1) There were approximately 275 bacteria after 2 hours
(2) k = 0.16



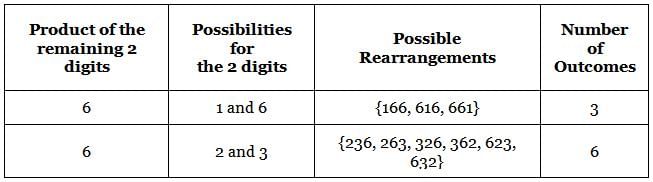
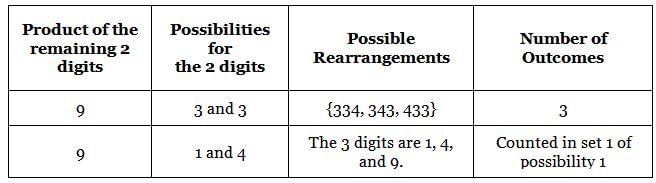
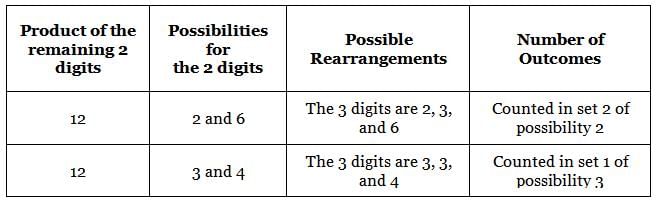
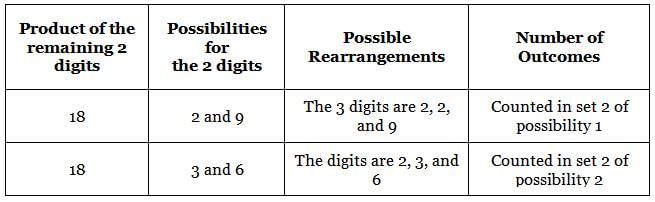
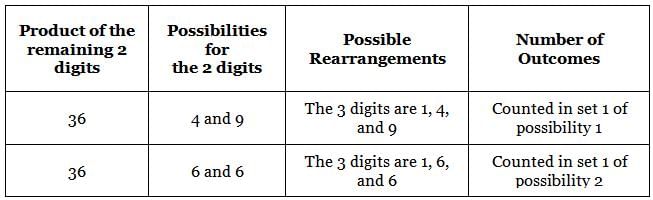
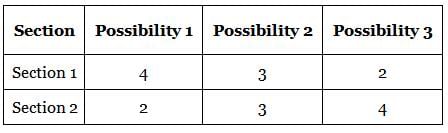
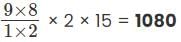
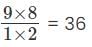 ways
ways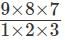 = 84 ways.
= 84 ways.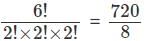 = 90 ways
= 90 ways