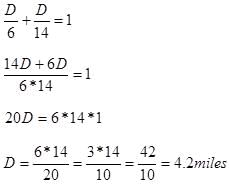GMAT Classic Mock Test - 9 - GMAT MCQ
30 Questions MCQ Test - GMAT Classic Mock Test - 9
Directions: Solve the problem and select the best of the answer choices given.
The City Opera House is expanding. Currently the city block containing the opera house is rectangular-shaped with a total volume of 9600 feet. If the expanded Opera House is 2.5 times as long, wide, and deep as the original building, what would the new volume be?
Directions: Solve the problem and select the best of the answer choices given.
In a university club of 200 people, the number of Political Science majors is 50 less than 4 times the number of International Relations majors. If one fifth of the club members are neither Political Science majors nor International Relations majors, and no club member is majoring in both Political Science and International Relations, how many of the club members are International Relations majors?
Directions: Solve the problem and select the best of the answer choices given.
If the total cost of 20 pairs of shoes is equal to the total revenue generated from the sale of 25 pairs of shoes, what is the percent of profit or loss made on the sale of each pair of shoes, assuming each pair of shoes cost the same dollar amount and each pair of shoes sold for the same dollar amount?
Directions: Solve the problem and select the best of the answer choices given.
Clarissa spent all day on a sightseeing trip in Britain. Starting from her hotel, Clarissa boarded a bus, which traveled at an average speed of 15 miles per hour through a 30 mile section of the countryside. The bus then stopped for lunch in London before continuing on a 3 hour tour of the city's sights at a speed of 10mph. Finally, the bus left the city and drove 40 miles straight back to the hotel. Clarissa arrived at her hotel exactly 2 hours after leaving London. What was the bus's average rate, approximately, for the entire journey?
Directions: Solve the problem and select the best of the answer choices given.
Meredith jogged to the top of a steep hill at an average pace of 6 miles per hour. She took the same trail back down. To her relief, the descent was much faster; her average speed rose to 14 miles per hour. If the entire run took Meredith exactly one hour to complete and she did not make any stops, how many miles, approximately, is the trail one way?
Directions: Solve the problem and select the best of the answer choices given.
At a medical research lab, nine doctors are conducting multiple clinical trials. Six of the doctors are working on a clinical trial with exactly one other doctor and three doctors are working on a clinical trial with exactly two other doctors. If two doctors are selected at random from the lab, what is the probability that those two doctors are NOT working together on a clinical trial?
Directions: Solve the problem and select the best of the answer choices given.
For which of the following functions g is g(z) = g(1 – z) for all z?
Directions: Solve the problem and select the best of the answer choices given.
A right triangle has sides that are consecutive even integers. The longest side is z. Which of the following equations could be used to find z?
Directions: Solve the problem and select the best of the answer choices given.
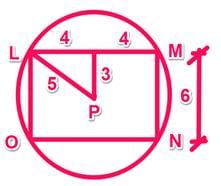
Rectangle LMNO is inscribed in a circle with center P. If the area of the rectangle is 8 times its width, and the distance from P to side LM is 3, what is the circle’s approximate circumference?
Directions: Solve the problem and select the best of the answer choices given.
Larry’s Lawn Service charges $w/hour for the first x hours of grass trimming, then w + 2 dollars for every hour of work over x hours. How much more will a homeowner be charged for a grass trimming job that took z hours if z > x than for a job which took only w hours if x < w < z?
Directions: Solve the problem and select the best of the answer choices given.
Lady Edith bought several necklaces at the jewelry store, and each necklace cost 16 dollars. Lady Mary also purchased several necklaces, at a cost of $20 each. If the ratio of the number of necklaces Lady Edith purchased to the number of necklaces Lady Mary purchased is 3 to 2, what is the average cost of the necklaces purchased by Lady Edith and Lady Mary?
Matthew, Jared, and Richard all bought flowers. The number of flowers Matthew purchased was equal to a single digit. Of the numbers of flowers purchased by Matthew, Jared, and Richard, only one was divisible by 3. The number of flowers one of them bought was an even number. Which of the following could represent the numbers of flowers each purchased?
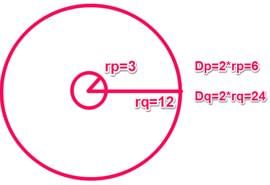
Circle P is inside Circle Q, and the two circles share the same center X. If the circumference of Q is four times the circumference of P, and the radius of Circle P is three, what is the difference between Circle Q’s diameter and Circle P’s diameter?
A yellow taxi cab went from Downtown to the Beachside and back at an average speed of 2/3 miles per hour. If the distance from Beachside to Downtown is 1 mile, and the trip back took half as much time as the trip there, what was the average speed of the yellow taxi cab on the way to Beachside?
Directions: Solve the problem and select the best of the answer choices given.
Circle B’s diameter was multiplied by 1.8. By what percent, approximately, was the area increased?
In ΔXYZ, what is the length of YZ?
Statement 1: The length of XY is 3
Statement 2: The length of XZ is 5.
The Embeyay Expressway and Emefay Expressway intersect at a perpendicular junction coming from Ulster City and Finster Town, respectively, while a direct road connecting the two municipalities is entirely straight. How much further would a motorist traveling the expressways between Ulster City to Finster Town have to drive in comparison to another motorist who used the direct road?
Statement 1: The distance from Ulster City to the Embeyay Expressway and Emefay Expressway junction is 12 kilometers.
Statement 2: The distance from Ulster City to Finster Town on the direct road is 15 kilometers.
If x, y, and z are positive numbers, is x > y > z?
Statement 1: xz > yz
Statement 2: yx > yz
If line d in the coordinate plane has the equation y=mx+b, where m and b are constants, what is the slope of line d?
(1) Line d intersects the line with equation y=6x+2 at the point (1, 8).
(2) Line d is parallel to the line with equation y=(2–m)x+b–4.
If x2 + y2 = 29, what is the value of (x - y)2 ?
Statement 1: xy = 10
Statement 2: X= 5
A={2,4,6,8,10,12,...}
B={3,6,9,12,15,18...}
True or false: n∈A∪B
Statement 1: n is a perfect square.
Statement 2: n is a multiple of 99.
Is x between O and 1 ?
Statement 1: x2 is less than x.
Statement 2: x3 1 s positive.
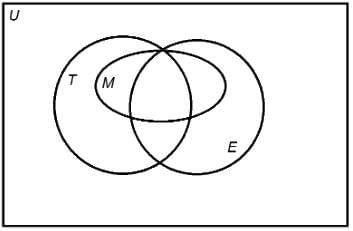
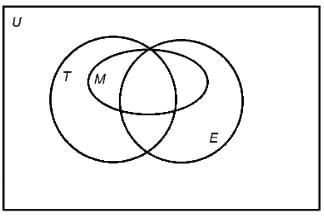
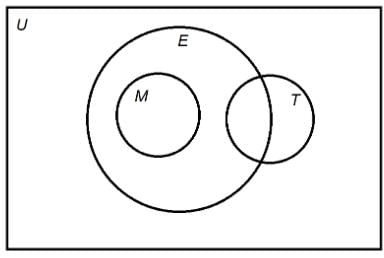
In the above Venn diagram, universal set U represents the residents of Jacksonville. The sets T,E,M represent the set of all Toastmasters, Elks, and Masons, respectively.
Jimmy is a resident of Jacksonville. Is Jimmy a Mason?
Statement 1: Jimmy is not a Toastmaster.
Statement 2: Jimmy is not an Elk.
What is the value of xy?
Statement 1: x + y = 10
Statement 2: x - y = 6
In the above Venn diagram, universal set U represents the residents of Eastland. The sets T,E,M represent the set of all Toastmasters, Elks, and Masons, respectively.
Craig is a resident of Eastland. Is Craig a Toastmaster?
Statement 1: Craig is not a Mason.
Statement 2: Craig is not an Elk.

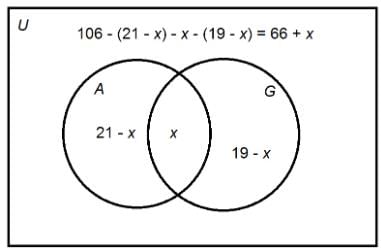
Two of the courses from which the 106 freshmen at Jefferson Academy may choose are American literature and German.
How many freshmen enrolled in both courses?
Statement 1: 19 freshment enrolled in German.
Statement 2: 21 freshmen enrolled in American literature.
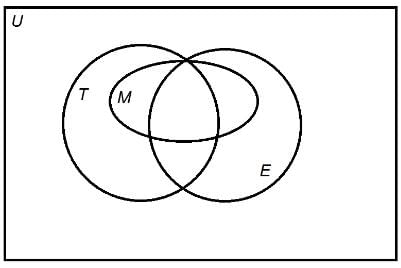
In the above Venn diagram, universal set U represents the residents of Wayne. The sets T,E,M represent the set of all teenagers, those with an even birth month, and males, respectively.
Is x2 greater than x?
Statement 1: x2 is greater than 1.
Statement 2: x is greater than -1.
If xy > 0, does (x - l)(y - 1) = 1 ?
Statement 1: x + y = xy
Statement 2: x = y
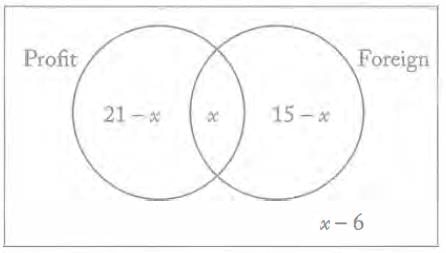
Last year in a group of 30 businesses, 21 reported a net profit and 15 had investments in foreign markets. How many of the businesses did not report a net profit nor invest in foreign markets last year?
Statement 1: Last year 12 of the 30 businesses reported a net profit and had investments in foreign markets.
Statement 2: Last year 24 of the 30 businesses reported a net profit or invested in foreign markets, or both.