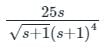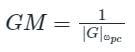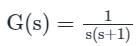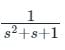Test: Nyquist Plot - 2 - Electrical Engineering (EE) MCQ
10 Questions MCQ Test - Test: Nyquist Plot - 2
A single-input single-output feedback system has forward transfer function G(s) and feedback transfer function H(s). It is given that |G(s)H(s)| < 1. Which of the following is true about the stability of the system?
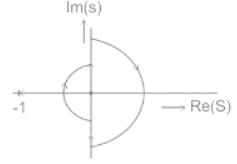
From the below given Nyquist plot, calculate the number of open-loop poles on the right-hand side of the s-plane for the closed-loop system to be stable.

The most important technique used for stability and the transient response of the system is
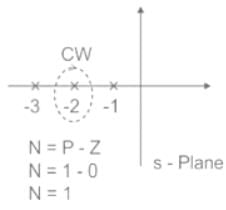
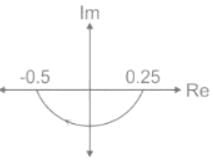
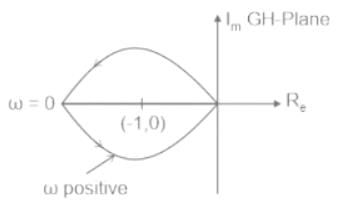
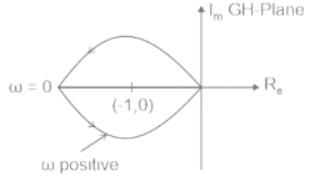
The number and direction of encirclements around the point −1+j0 in the complex plane by the Nyquist plot of 
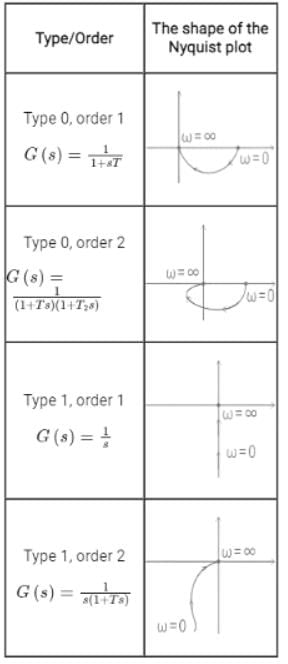
In Nyquist plot of a system on adding a pole at s = 0, then plot will -
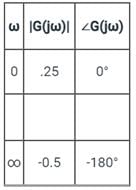
The frequency at which the Nyquist plot of a unity feedback system with the open loop transfer function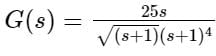 crosses the negative real axis is
crosses the negative real axis is
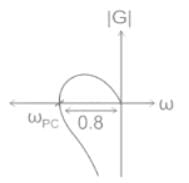
If the Nyquist plot cuts the negative real axis at a distance of 0.8, then the gain margin of the system is
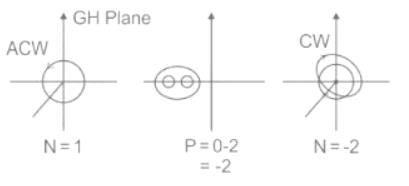
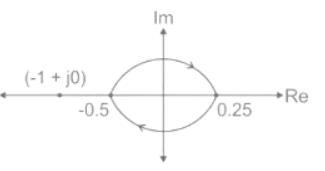
The figure shows the Nyquist plot of the open-loop transfer function G(s)H(s) of a system. If G(s)H(s) has one right-hand pole, the closed-loop system is
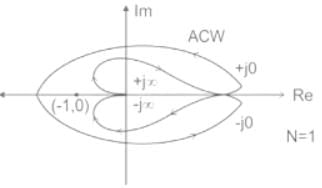
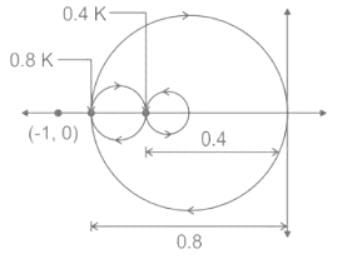
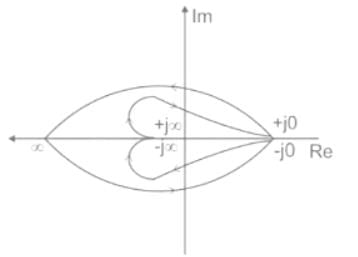
Consider a closed-loop control system with unity negative feedback and KG(s) in the forward path, where the gain K = 2. The complete Nyquist plot of the transfer function G(s) is shown in the figure. Note that the Nyquist contour has been chosen to have the clockwise sense. Assume G(s) has no poles on the closed right-half of the complex plane. The number of poles of the closed-loop transfer function in the closed right-half of the complex plane is ___________.

The open loop transfer function of a unity gain negative feedback system is given as
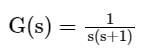
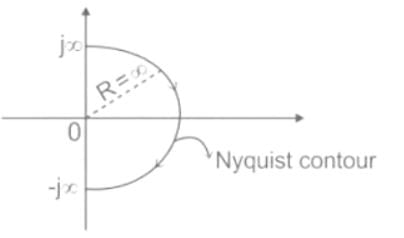
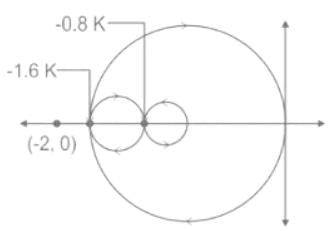
The Nyquist contour in the ��-plane encloses the entire right half plane and a small neighbourhood around the origin in the left half plane, as shown in the figure below. The number of encirclements of the point (−1 + j0) by the Nyquist plot of G(s), corresponding to the Nyquist contour, is denoted as N. Then N equals to