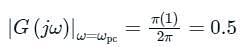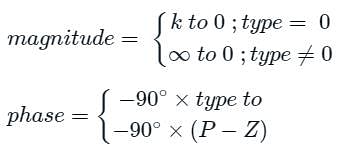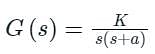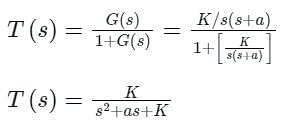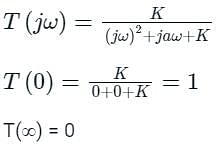Test: Nyquist Plot - 3 - Electrical Engineering (EE) MCQ
10 Questions MCQ Test - Test: Nyquist Plot - 3
______indicates not only whether a system is stable, but also its degree of stability and how stability may be imposed if necessary.
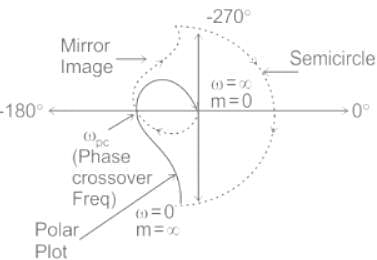
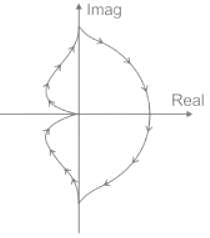
The loop transfer function of a negative feedback system is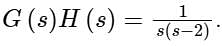 The Nyquist plot for the above system
The Nyquist plot for the above system
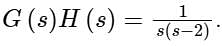 The Nyquist plot for the above system
The Nyquist plot for the above system| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
The open loop transfer function of a unity feedback system is given by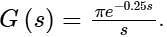 In G(s) plane, the Nyquist plot of G(s) passes through the negative real axis at the point
In G(s) plane, the Nyquist plot of G(s) passes through the negative real axis at the point
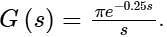 In G(s) plane, the Nyquist plot of G(s) passes through the negative real axis at the point
In G(s) plane, the Nyquist plot of G(s) passes through the negative real axis at the pointConsider a unity feedback system whose open loop transfer function is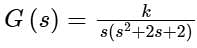 The Nyquist plot for this system is
The Nyquist plot for this system is
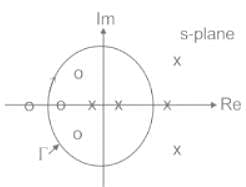
The pole-zero map of a rational function G(s) is shown below. When the closed contour Γ is mapped into the G(s)-plane, then the mapping encircles
For the transfer function G (jω) = 5 + jω, the corresponding Nyquist plot for positive frequency has the form
The Nyquist stability criterion and the Routh criterion both are powerful analysis tools for determining the stability of feedback controllers. Identify which of the following statements is FALSE:
The Nyquist plot of the transfer function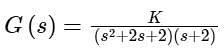 Does not encircle the point (–1 + j0) for K = 10 but does encircle the point (-1 + j0) for K = 100 . Then the closed-loop system (having unity gain feedback) is
Does not encircle the point (–1 + j0) for K = 10 but does encircle the point (-1 + j0) for K = 100 . Then the closed-loop system (having unity gain feedback) is
The complete Nyquist plot of the open-loop transfer function G(s) H(s) of a feedback control system is shown in the figure.

If G(s) H(s) has one zero in the right-half of the s-plane. the number of poles that the closed-loop system will have in the right-half of the s-plane is
Which of the following is a powerful frequency-domain method of extracting the information regarding stability as well as the relative stability of a system without the need to evaluate the roots of the characteristic equation?