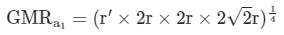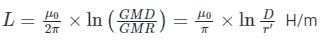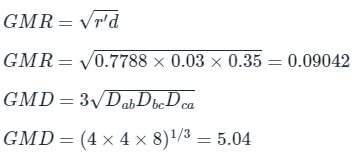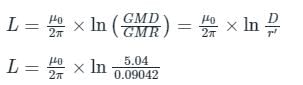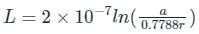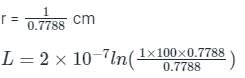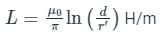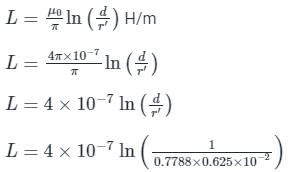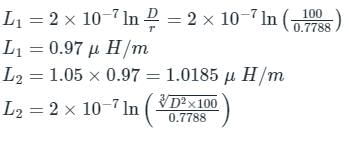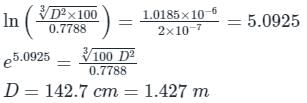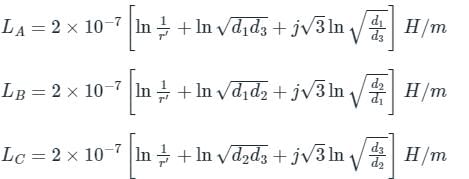Test: Calculation of Inductance of Transmission Line - Electrical Engineering (EE) MCQ
10 Questions MCQ Test - Test: Calculation of Inductance of Transmission Line
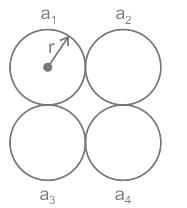
The geometric mean radius of a conductor, having four equal strands with each strand of radius ‘r’, as shown in the figure below, is

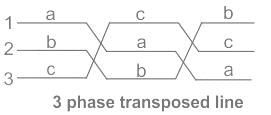
(I) Unsymmetrical spacing configurations cause the line interference.
(II) Unsymmetrical spacing causes the voltage induction in the communication lines.
The above problems can be eliminated by ________
(II) Unsymmetrical spacing causes the voltage induction in the communication lines.
The above problems can be eliminated by ________
The inductance of a power transmission line increases with
If the height of transmission tower is increased:
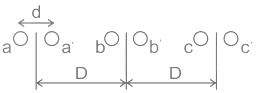
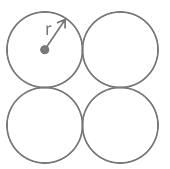
Refer to the following figure; the radius of each conductor is 0.03 m. It is also known that the spacing between phase conductors is 35 cm and the distance between the phases (D) is 4 m. Find the value of the average inductance of three-phase line arranged.
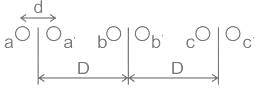
A three-phase line has its conductors at the corners of an equilateral triangle of side 1 m. The radius of each conductor is (1/0.7788) cm. The inductance per phase per km is given by:
A single-phase transmission line consists of two parallel conductors one meter apart and 1.25 cm in diameter. The loop inductance per km of the line is:
Consider an overhead transmission line with 3-phase, 50 Hz balanced system with conductors located at the vertices of an equilateral triangle of length Dab = Dbc = Dca = 1 m as shown in figure below. The resistances of the conductors are neglected. The geometric mean radius (GMR) of each conductor is 0.01 m. Neglecting the effect of ground, the magnitude of positive sequence reactance in Ω/km (rounded off to three decimal places) is _________
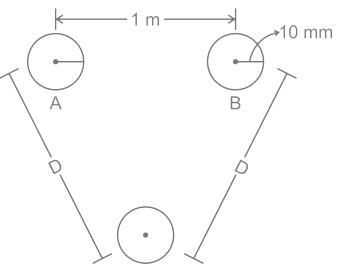
A single-phase transmission line has two conductors each of 10mm radius. These are fixed at a center-to-center distance of 1m in a horizontal plane. This is now converted to a three-phase transmission line by introducing a third conductor of the same radius. This conductor is fixed at an equal distance D from the two single-phase conductors. The three-phase line is fully transposed. The positive sequence inductance per phase of the three-phase system is to be 5% more than that of the inductance per conductor of the single-phase system. The distance D, in meters, is _______.
Directions: It consists of two statements, one labeled as the ‘Statement (I)’ and the other as ‘Statement (II)’. Examine these two statements carefully and select the answer using the codes given below:
Statement (I): The expression for the value of inductance L per conductor of an unsymmetrically spaced 3-phase overhead transmission line contains an imaginary term.
Statement (II): The presence of the imaginary term is due to the mutual inductance between the phase conductors and can be eliminated by symmetrically transposing the three line-conductors along the length of the line.