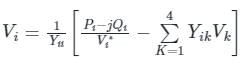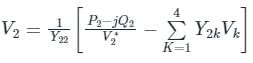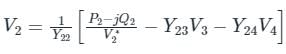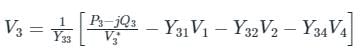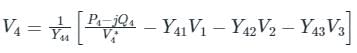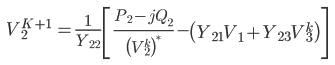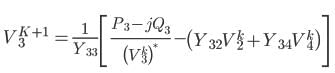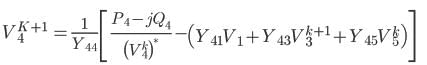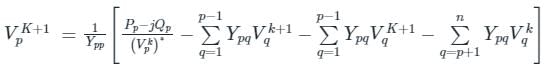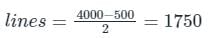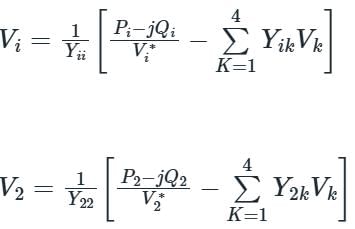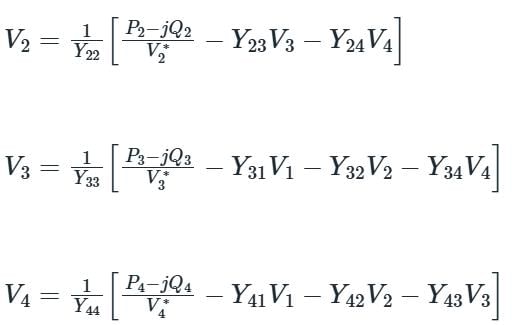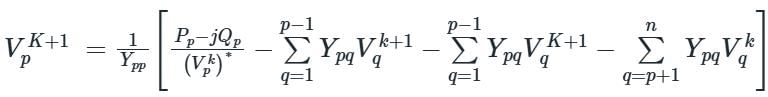Test: Gauss-Siedel Method - Electrical Engineering (EE) MCQ
10 Questions MCQ Test - Test: Gauss-Siedel Method
In G - S method of power flow problem, the number of iterations
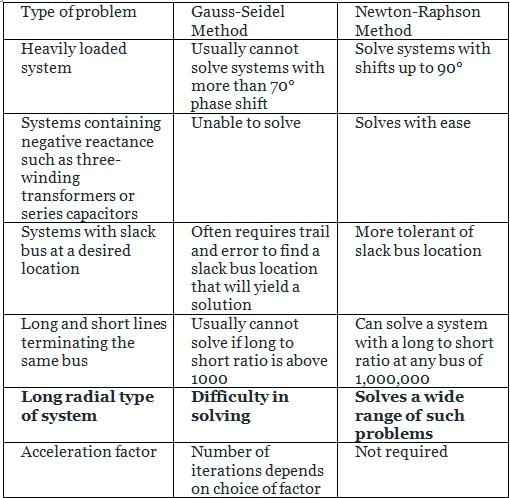
In comparison to Gauss Seidel, Newton Raphson method takes
Which of the following has a problem in convergence for a system with long radial lines?
Number of iterations required for convergence of a load flow algorithm increases significantly with increase of number of buses with
A 500 × 500 bus admittance matrix for an electric power system 4000 non-zero elements the minimum number of branches in this system are –
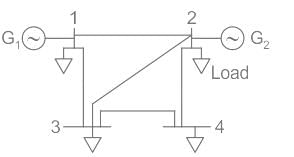
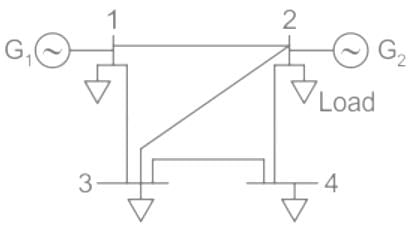
For the set of linear equations given below, what is the value of voltage V1 after first iteration of Gauss Siedal method? Assume the initial approximation is V1 = 0
10V1 + 2V2 = 10, 4V1 + 7V2 = 15
In Gauss Seidel method of power flow problem the number of iterations may be reduced if the correction in voltage at each bus is multiplied by
If the reference bus is changed in two load flow runs with same system data and power obtained for reference bus taken as specified P and Q in the latter run
The Gauss Seidel load flow method has following disadvantages. Mark the incorrect statement
In G - S method of power flow problem, the number of iterations