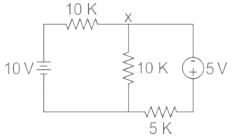
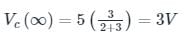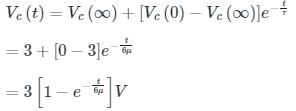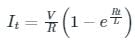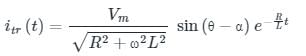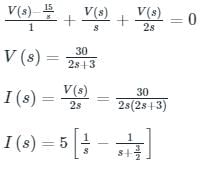Test: Step Response of First Order Circuits - 2 - Electrical Engineering (EE) MCQ
10 Questions MCQ Test - Test: Step Response of First Order Circuits - 2
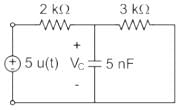
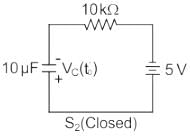
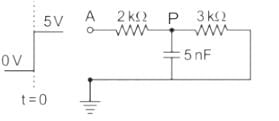
In the circuit shown below, a step input voltage of magnitude 5 V is applied at node A at time t = 0. If the capacitor has no charge for t < 0, the voltage at node P at t = 6 μs is ________ V. (Answer should be rounded off to two decimal places)

In a series RL circuit the value of inductance is 1 Henry and resistance is 10 ohms. What is the time constant of the circuit?
First order system is defined as :
The transfer function of the system is G(s) = 100/(s + 1) (s + 100). For a unit step input to the system the approximate settling time for 2% criterion is:
A first order system and its response to a unit step input are shown in figure below. The system parameters are____________
Calculate the peak value of the source voltage (in V) if the root-mean square voltage across the resistor and inductor in a series RL circuit is 13 V and 12 V, respectively.
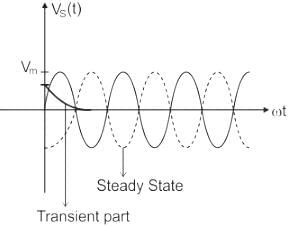
In an R-L circuit connected to an alternating sinusoidal voltage, size of transient current primarily depends on:
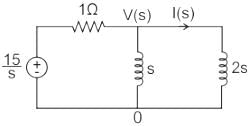
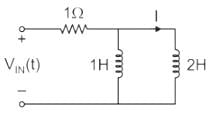
In the circuit shown, the voltage VIN(t) is described by:
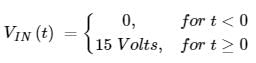
where t is in seconds. The time (in seconds) at which the current I in the circuit will reach the value 2 Amperes is ________.
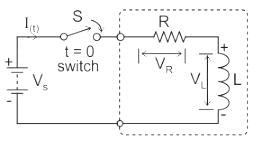
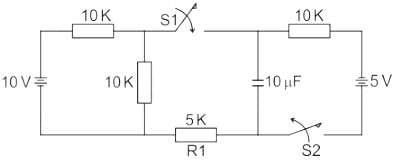
In the circuit shown below, switch S1 and S2 are in open and close position respectively for long time. At t = t0, switch S1 is closed and switch S2 is opened. What would be the current through R1 immediately after the transition of switches?
Assertion (A.: It is observed that step function is first derivative of a ramp function and impulse function is first derivative of a step function.
Reason (R): From the derived time response expression it is concluded that the output time response also follows the same sequence as that of input functions.