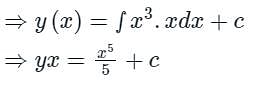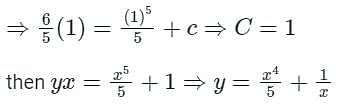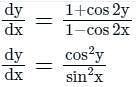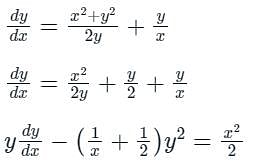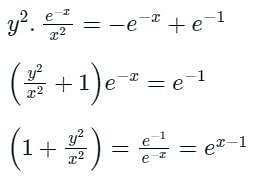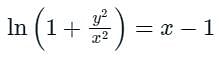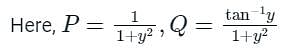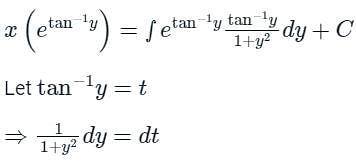Test: First Order Differential Equations - 1 - Electronics and Communication Engineering (ECE) MCQ
10 Questions MCQ Test - Test: First Order Differential Equations - 1
Second Derivative of sin(x) with respect to x is
The derivative of f(x) = cos(x) can be estimated using the approximation The percentage error is calculated as
The percentage error is calculated as The percentage error in the derivative of f(x) at x = π/6 radian, choosing h = 0.1 radian, is
The percentage error in the derivative of f(x) at x = π/6 radian, choosing h = 0.1 radian, is
 The percentage error is calculated as
The percentage error is calculated as The percentage error in the derivative of f(x) at x = π/6 radian, choosing h = 0.1 radian, is
The percentage error in the derivative of f(x) at x = π/6 radian, choosing h = 0.1 radian, is| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
A differential equation did is applicable over −10 < t < 10. If i(4) = 10, then i(−5) is _______. (Important - Enter only the numerical value in the answer)
is applicable over −10 < t < 10. If i(4) = 10, then i(−5) is _______. (Important - Enter only the numerical value in the answer)
 is applicable over −10 < t < 10. If i(4) = 10, then i(−5) is _______. (Important - Enter only the numerical value in the answer)
is applicable over −10 < t < 10. If i(4) = 10, then i(−5) is _______. (Important - Enter only the numerical value in the answer)The families of curves represented by the solution of the equation
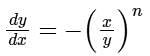
for n = −1 and n = +1, respectively, are
Given the ordinary differential equation With y (0) = 0 and
With y (0) = 0 and , the value of y(1) is ______ (correct to two decimal places). (Important - Enter only the numerical value in the answer)
, the value of y(1) is ______ (correct to two decimal places). (Important - Enter only the numerical value in the answer)
What is the complete solution for the equation x (y - z) p + y (z - x) q = z (x - y)?
The solution of with the condition y(1) = 6/5 is
with the condition y(1) = 6/5 is
The general solution of the differential equation
A curve passes through the point (x = 1, y = 0) and satisfies the differential equation The equation that describes the curve is
The equation that describes the curve is
The solution of the differential equation (1 + y2)dx = (tan-1 y - x)dy is








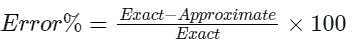
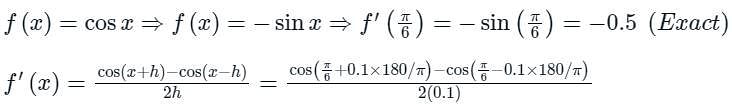





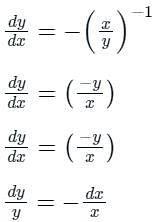

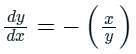





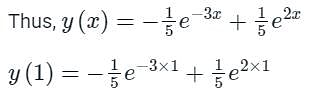
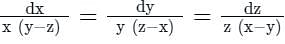
 , it can be written as
, it can be written as 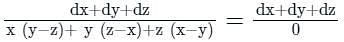
 we get,
we get,