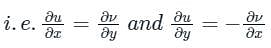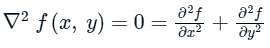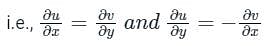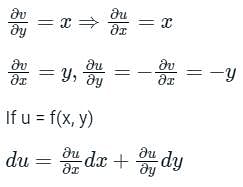Test: Analytic Functions - 2 - Civil Engineering (CE) MCQ
10 Questions MCQ Test - Test: Analytic Functions - 2
The function f(x, y) satisfies the Laplace equation
∇2f(x,y)=0
on a circular domain of radius r = 1 with its center at point P with coordinates x = 0, y = 0. The value of this function on the circular boundary of this domain is equal to 3.
The numerical value of f(0, 0) is:
∇2f(x,y)=0
on a circular domain of radius r = 1 with its center at point P with coordinates x = 0, y = 0. The value of this function on the circular boundary of this domain is equal to 3.
The numerical value of f(0, 0) is:
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Which one of the following functions is analytic in the region |z| ≤ 1?
The only function among the following that is analytic, is
Given two complex numbers Z1 = 5 + (5√3)i, and Z2 = 2/√3 + 2i the argument of Z1/Z2 in degrees is
The real part of an analytic function f(z) where z = x + iy is given by e-y cos (x). The imaginary part of f(z) is
A harmonic function is analytic if it satisfies the Laplace equation. If u(x, y) = 2x2 − 2y2 + 4xy is a harmonic function, then its conjugate harmonic function v(x, y) is
What is the value of m for which 2x – x2 + my2 is harmonic?
f(z) = u(x, y) + iv(x, y) is an analytic function of complex variable z = x + iy. If v = xy then u(x, y) equals
If u = x2 – y2, then the conjugate harmonic function is


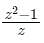
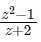
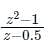
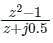

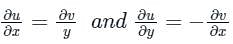 Calculation:
Calculation: