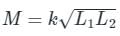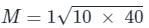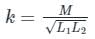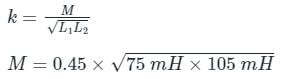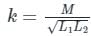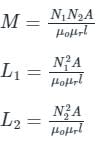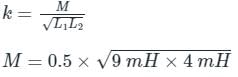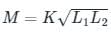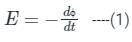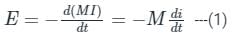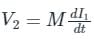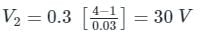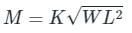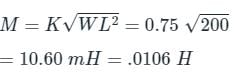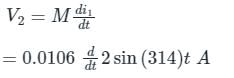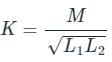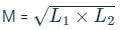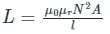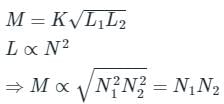Test: Mutual Inductance - 2 - Electronics and Communication Engineering (ECE) MCQ
10 Questions MCQ Test - Test: Mutual Inductance - 2
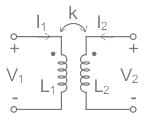
Two coils having self-inductances of 10 mH and 40 mH are mutually coupled. What is the maximum possible mutual inductance?
The coefficient of coupling between two coils is 0.45. The first coil has an inductance of 75 mH and the second coil has an inductance of 105 mH. What is the mutual inductance between the coils?
The self inductance of two coils are 4mH and 9mH respectively. If the coefficient of coupling is 0.5, the mutual inductance between the coils is _____
The total inductance of two coupled coils in the ‘series aiding’ and ‘series opposing’ connections are 1.4 × 10-3 Henry and 0.6 × 10-3 Henry, respectively. The value of mutual inductance will be:
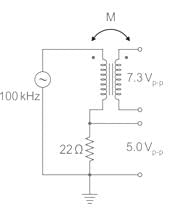
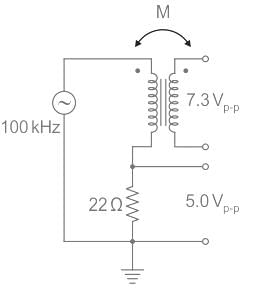
An air-core radio-frequency transformer as shown has a primary winding and a secondary winding. The mutual inductance M between the windings of the transformer is ______ μH.
(Round off to 2 decimal places.)
Determine the mutual inductance between two coils when a current changing at 20 A/s in one coil induces an EMF of 50 mV in the other.
Two inductive coils which are close to each other have a mutual inductance of 0.3 H. Current through one coil is increased from 1 A to 4 A in 0.03 s. The voltage induced in the other coil is:
Two coupled coils have self inductances L1 = 10 mH and L2 = 20 mH.
The co-efficient of coupling (K) being 0.75 in the air. Voltage in the second coil when the current in circuit is given by I = 2 sin (314t) A is _______
Two coils having self-inductance of L1 and L2, respectively, are magnetically coupled. The maximum possible value of mutual inductance between the coils is
Mutual inductance between two closely coupled coils is 2 H. Now, if the number of turns in one coil is reduced by 50 percent and those of the other coil is doubled then, new value of mutual inductance is: