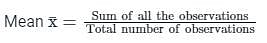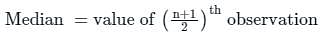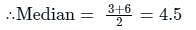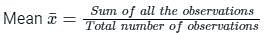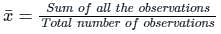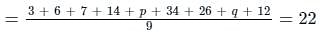Test: Measures of Central Tendency - 2 - Commerce MCQ
15 Questions MCQ Test - Test: Measures of Central Tendency - 2
Let x be the mean of squares of first n natural numbers and y be the square of mean of first n natural numbers. If x/y = 55/42, then what is the value of n ?
If a variable takes discrete values a + 4, a - 3.5, a - 2.5, a - 3, a - 2, a + 0.5, a + 5 and a - 0.5 where a > 0, then the median of the data set is
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Find the median of the given set of numbers 2, 6, 6, 8, 4, 2, 7, 9
If the mode of the following data is 7, then the value of k in the data set 3, 8, 6, 7, 1, 6, 10, 6, 7, 2k + 5, 9, 7, and 13 is:
Let the average of three numbers be 16. If two of the numbers are 8 and 10, what is the remaining number?
What is the mean of first 99 natural numbers ?
The mean of six numbers is 47. If one number is excluded, their mean becomes 41. The excluded number is
Find the median of the series of all the even terms from 4 to 296.
Find the value of ‘n’ if the mean of the set of the numbers 8, 5, n, 10, 15, 21 is given as 11.
Find the median of the data set: 6, 3, 8, 2, 9, 1?
Find the value ‘p + q’, if mean of set of numbers 3, 6, 7, 14, p, 34, 26, q, 12 is given as 22.
The mean of 25 observations is 36. If the mean of the first 13 observations is 32 and that of the last 13 observations is 39 , the 13th observation is:
What is the mean of the range, mode and median of the data given below?
5, 10, 3, 6, 4, 8, 9, 3, 15, 2, 9, 4, 19, 11, 4
If mean and mode of some data are 4 & 10 respectively, its median will be:


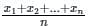
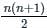
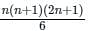
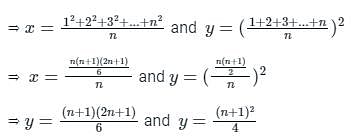
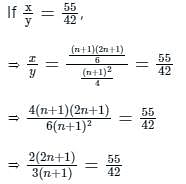
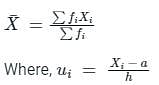
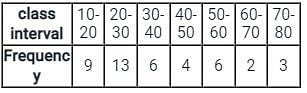
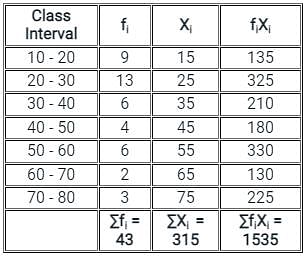
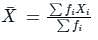

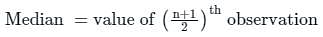



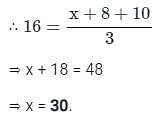
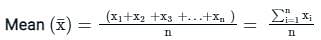
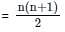
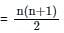
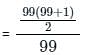
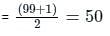

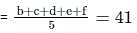
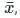 , read as ‘x bar’.
, read as ‘x bar’.