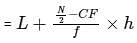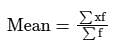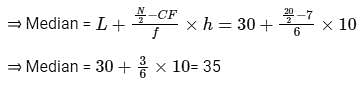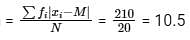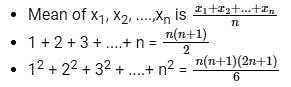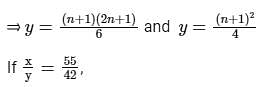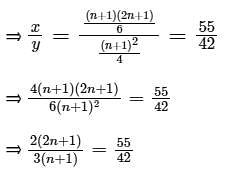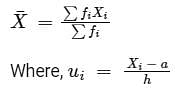Test: Measures of Central Tendency - Electronics and Communication Engineering (ECE) MCQ
10 Questions MCQ Test - Test: Measures of Central Tendency
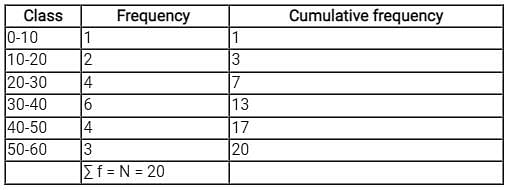
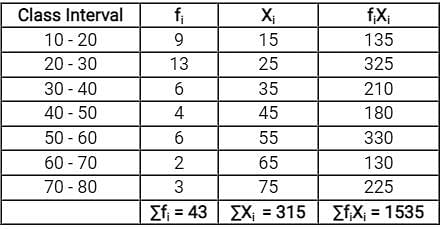
Consider the following grouped frequency distribution:

What is the median of the distribution ?

The mean of 25 observations is 36 . If the mean of the first 13 observations is 32 and that of the last 13 observations is 39 , the 13th observation is:
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
What is the mean of the range, mode and median of the data given below?
5, 10, 3, 6, 4, 8, 9, 3, 15, 2, 9, 4, 19, 11, 4
If mean and mode of some data are 4 & 10 respectively, its median will be:
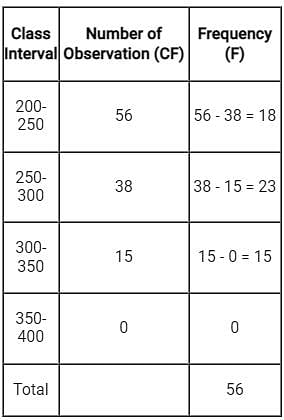
Find the no. of observations between 250 and 300 from the following data:

A random sample of 24 people is classified in the following table according to their ages:
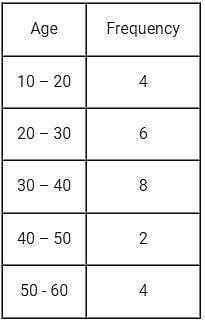
What is the mean age of this group of people?
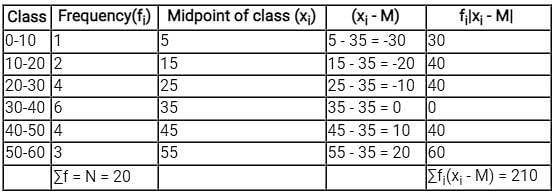
Consider the following grouped frequency distribution:

What is mean deviation about the median ?
Let x be the mean of squares of first n natural numbers and y be the square of mean of first n natural numbers. If x/y = 55/42 , then what is the value of n ?
If a variable takes discrete values a + 4, a - 3.5, a - 2.5, a - 3, a - 2, a + 0.5, a + 5 and a - 0.5 where a > 0, then the median of the data set is