Test (With calculator) - 1 - SAT MCQ
10 Questions MCQ Test - Test (With calculator) - 1
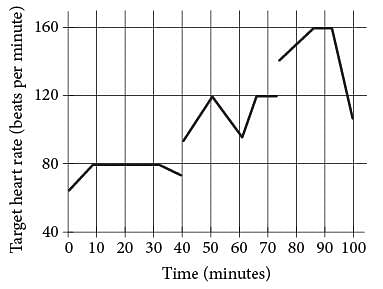
John runs at different speeds as part of his training program. The graph shows his target heart rate at different times during his workout. On which interval is the target heart rate strictly increasing then strictly decreasing?

If y = kx, where k is a constant, and y = 24 when x = 6, what is the value of y when x = 5?
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
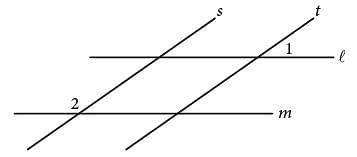
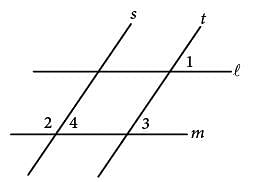
In the figure above, lines l and m are parallel and lines s and t are parallel. If the measure of ∠1 is 35°, what is the measure of ∠2?

In the figure above, lines l and m are parallel and lines s and t are parallel. If the measure of ∠1 is 35°, what is the measure of ∠2?
If 16 + 4x is 10 more than 14, what is the value of 8x?
Which of the following graphs best shows a strong negative association between d and t?
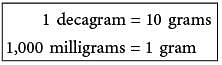
A hospital stores one type of medicine in 2-decagram containers. Based on the information given in the box above, how many 1-milligram doses are there in one 2-decagram container?
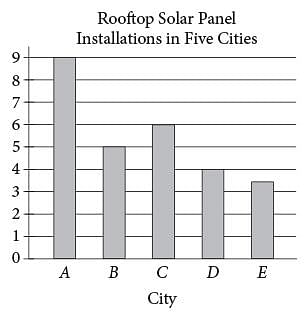
The number of rooftops with solar panel installations in 5 cities is shown in the graph above. If the total number of installations is 27,500, what is an appropriate label for the vertical axis of the graph?
Question refer to the following information.
a = 1,052 + 1.08t
The speed of a sound wave in air depends on the air temperature. The formula above shows the relationship between a, the speed of a sound wave, in feet per second, and t, the air temperature, in degrees Fahrenheit (°F).
Which of the following expresses the air temperature in terms of the speed of a sound wave?
Question refer to the following information.
a = 1,052 + 1.08t
The speed of a sound wave in air depends on the air temperature. The formula above shows the relationship between a, the speed of a sound wave, in feet per second, and t, the air temperature, in degrees Fahrenheit (°F).
At which of the following air temperatures will the speed of a sound wave be closest to 1,000 feet per second?


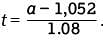
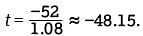 Of the choices given, -48°F is closest to -48.15°F.
Of the choices given, -48°F is closest to -48.15°F.














