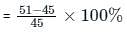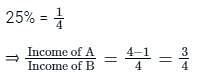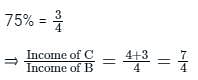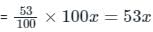Practice Test: Percentages- 2 - JAMB MCQ
15 Questions MCQ Test - Practice Test: Percentages- 2
A glass of juice contains 5% fruit extract, 25% of pulp and rest of water. Find amount of water that should be added in glass of 450 ml juice to reduce pulp concentration to 15%?
In an election A got 55% of the total votes and the remaining votes were casted to B. If 10,000 votes of A are given to B, there would have been a tie. Find the number of total votes polled?
65% of a number is more than 25% of the number by 120. What is 20% of that number?
Out of two numbers, 65% of the smaller number is equal to 45% of the larger number. If the sum of two numbers is 2574, then what is the value of the larger number?
Two students appeared for an examination. One of them secured 22 marks more than the other and his marks were 55% of the sum of their marks. The marks obtained by them are _______.
The weighing machine at Nathan’s shop is a faulty one. It shows 20% less than the actual weight put on it. However, it shows wrong weight only in some cases with a probability ranging between 0.4 to 0.6. Assuming that Nathan sells at cost price, what could be the maximum loss that Nathan can face? (Assume Nathan sells equal quantity in each transaction)
Ted spends 55% of his income. His income increases by 28% and his expenditure also increases by 40%. The percentage of increase in his savings is:
The income of A is 25% less than the income of B and the income of C is 75% more than the income of B. If the difference in the income of A and C is Rs. 100, then find the income of B.
A solution contains 33g of common salt in 320g of water. Calculate the concentration in terms of mass, by mass percentage of the solution.
There were two candidates in an election, 10% of voters did not vote and 48 votes were found invalid. The winning candidate got 53% of all the voters in the list and won by 304 votes. Find the total number of votes enrolled.
If the price of petrol has increased from Rs. 40 per litre to Rs. 60 per litre, by how much percent a person has to decrease his consumption so that his expenditure remains same.
If the average, of a given number, 50% of that number and 25% of the same number is 280, then the number is
A fruit seller sells 45% of the oranges that he has along with one more orange to a customer. He then sells 20% of the remaining oranges and 2 more oranges to a second customer. He then sells 90% of the now remaining oranges to a third customer and is still left with 5 oranges. How many oranges did the fruit seller have initially?
The income of Doyel is 40% more than that of Chitra. Chitra got an 8% hike in his income, and Doyel got a 25% hike in her income. The percentage increase in their combined income is:
An engineering student has to secure 15% marks to pass. He gets 55 marks and fails by 20 marks. Find his maximum marks.