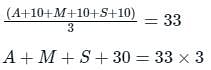Test: Puzzle (पहेली परीक्षण) - SSC MCQ
10 Questions MCQ Test - Test: Puzzle (पहेली परीक्षण)
पिता और पुत्र की आयु का योग 50 है। छह साल पहले पिता की आयु बेटे की आयु के 3 गुना से 6 अधिक थी। 6 साल बाद पिता की आयु क्या होगी?
छह वर्ष पहले P और Q की आयु का अनुपात 6: 5 था। चार वर्ष बाद यह 11 : 10 होगा। P की आयु अब क्या है?
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
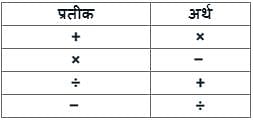
यदि + का अर्थ ×, × का अर्थ - , ÷ का अर्थ +, और - का अर्थ ÷ है , तो,
146 - 2 + 3 × 123 × 5 + 2 =?
146 - 2 + 3 × 123 × 5 + 2 =?
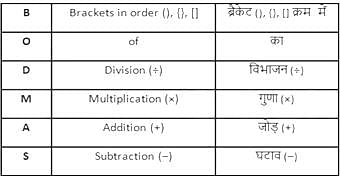
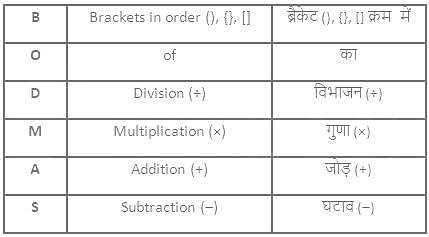
BODMAS नियम का प्रयोग करके हल कीजिए।
34 + 16 ÷ 2 × 3 + 5 ÷ 15 × 9 - 6 + 8
एक बैग में 186 रुपये की राशि के 50 पैसे, 25 पैसे और 10 पैसे के सिक्कों का अनुपात 12 : 8 : 13 हैं। प्रत्येक प्रकार के सिक्कों की संख्या ज्ञात कीजिए।
बैल और मुर्गियों के समूह में, पैरों की संख्या, सिर की संख्या की दोगुनी से 48 अधिक है। बैलो की संख्या ________ है।
1 जनवरी, 2015 को अमित, महेश और रमेश की कुल आयु 108 है। महेश, अमित से तीन साल छोटा है। रमेश, महेश के पिता हैं और उनकी औसत आयु 42 है। 1 जनवरी, 2010 को रमेश की आयु क्या थी?
निम्नलिखित समीकरण को सही बनाने के लिए किन दो चिन्हों को आपस में बदला जाना चाहिए? 21 + 5 × 2 – 21 ÷ 3 = 12
खिलाड़ियों की कुल संख्या में से, 100/3% होटल X में हैं और शेष होटल Y में हैं। यदि होटल Y से 20 खिलाड़ियों को होटल X में स्थानांतरित कर दिया जाता है, तो होटल X में खिलाड़ियों की संख्या खिलाड़ियों की कुल संख्या का 50% हो जाती है। यदि होटल X के 20 खिलाड़ियों को होटल Y में स्थानांतरित कर दिया जाता है, तो होटल X में खिलाड़ियों की संख्या खिलाड़ियों की कुल संख्या का कितना प्रतिशत हो जाती है?
अभी से सात वर्षों के बाद, अनामिका की आयु, 4 वर्ष पहले मालिनी की आयु के बराबर होगी। श्रीनिधि का जन्म 2 वर्ष पहले हुआ था। अभी से 10 वर्षों के बाद अनामिका, मालिनी और श्रीनिधि की औसत आयु 33 वर्ष होगी। अनामिका की वर्तमान आयु क्या है?