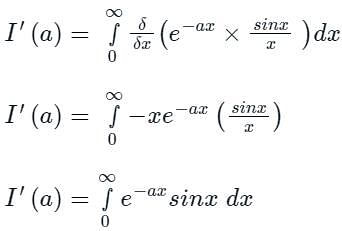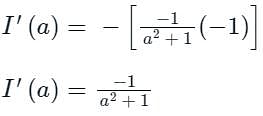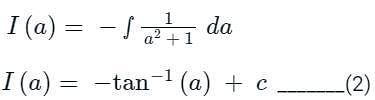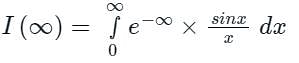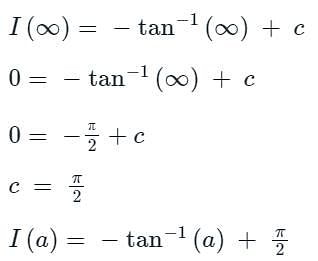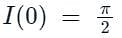Test: Fourier Series- 1 - Civil Engineering (CE) MCQ
10 Questions MCQ Test - Test: Fourier Series- 1
The Fourier series expansion of x3 in the interval −1 ≤ x < 1 with periodic continuation has
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
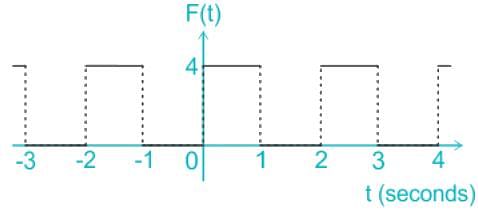
F(t) is a periodic square wave function as shown. It takes only two values, 4 and 0, and stays at each of these values for 1 second before changing. What is the constant term in the Fourier series expansion of F(t)?

The Fourier series is given by 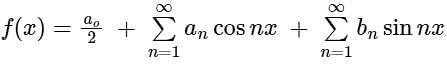 in the interval -π < x < π.
in the interval -π < x < π.
Which among the following is true?
The Fourier series expansion of the saw-toothed waveform f(x) = x in (- π, π) of period 2π gives the series, 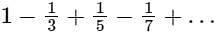
The sum is equal to
The Fourier series expansion of x3 in the interval −1 ≤ x < 1 with periodic continuation has
Let \(f\left( x \right) = \;\left\{ {\begin{array}{*{20}{c}} { - π }&{if\;}&{ - π
be a periodic function of period 2π. The coefficient of sin 5x in the Fourier series expansion of f(x) in the interval [-π, π] is


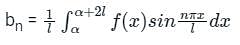
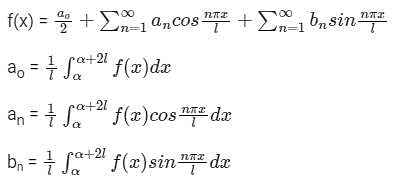
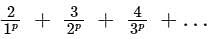 will be
will be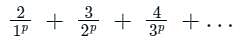
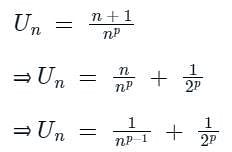
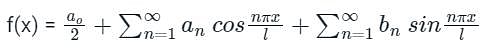
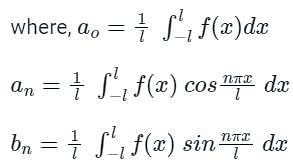
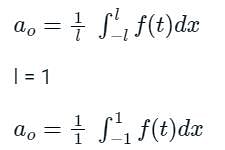
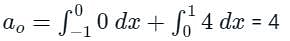
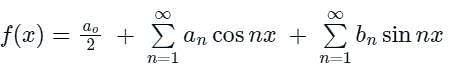
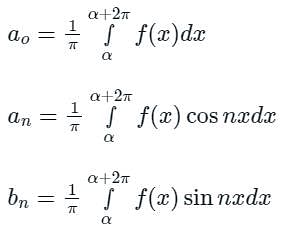
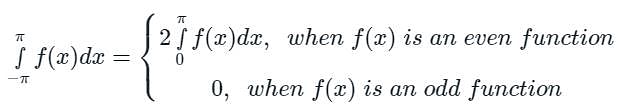
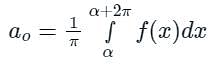
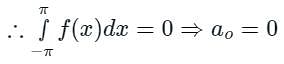 [Option 1 is correct].
[Option 1 is correct].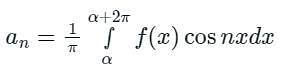
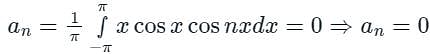 [Option 2 is correct].
[Option 2 is correct].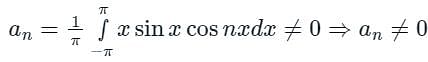 [Option 3 is incorrect].
[Option 3 is incorrect]. [Option 4 is correct].
[Option 4 is correct].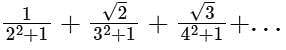 is-
is-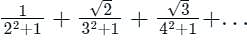
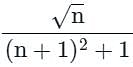
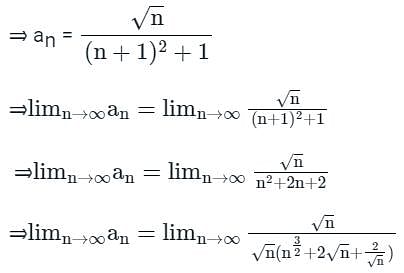
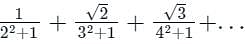 is convergent.
is convergent.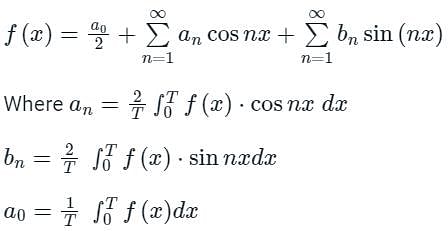


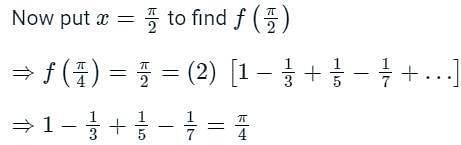
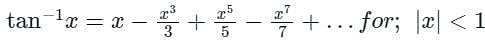
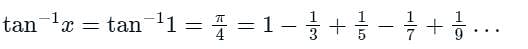
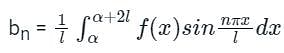
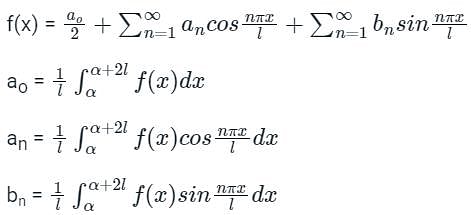
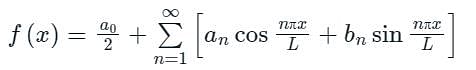
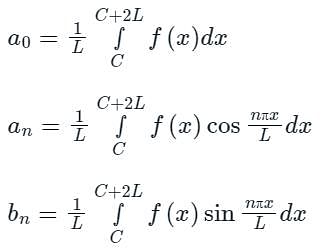

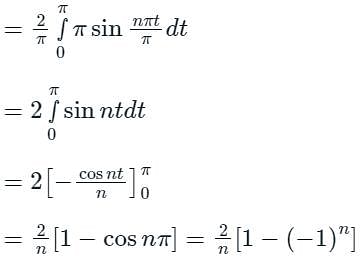
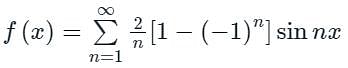
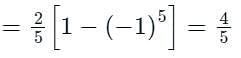
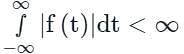
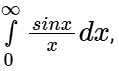 Then the integral
Then the integral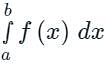 is said to be the improper integral of the first kind if a = -∞ or b = ∞ or both.
is said to be the improper integral of the first kind if a = -∞ or b = ∞ or both.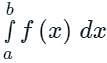 is said to be the improper integral of the second kind if a or b is finite but f(x) is infinite for some x ∈ [a, b].
is said to be the improper integral of the second kind if a or b is finite but f(x) is infinite for some x ∈ [a, b].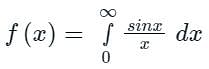
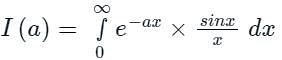 ...(1)
...(1)