Electronics and Communication Engineering (ECE) Exam > Electronics and Communication Engineering (ECE) Tests > Test: Wave Equation - Electronics and Communication Engineering (ECE) MCQ
Test: Wave Equation - Electronics and Communication Engineering (ECE) MCQ
Test Description
10 Questions MCQ Test - Test: Wave Equation
Test: Wave Equation for Electronics and Communication Engineering (ECE) 2024 is part of Electronics and Communication Engineering (ECE) preparation. The Test: Wave Equation questions and answers have been prepared
according to the Electronics and Communication Engineering (ECE) exam syllabus.The Test: Wave Equation MCQs are made for Electronics and Communication Engineering (ECE) 2024 Exam.
Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests for Test: Wave Equation below.
Solutions of Test: Wave Equation questions in English are available as part of our course for Electronics and Communication Engineering (ECE) & Test: Wave Equation solutions in
Hindi for Electronics and Communication Engineering (ECE) course.
Download more important topics, notes, lectures and mock test series for Electronics and Communication Engineering (ECE) Exam by signing up for free. Attempt Test: Wave Equation | 10 questions in 30 minutes | Mock test for Electronics and Communication Engineering (ECE) preparation | Free important questions MCQ to study for Electronics and Communication Engineering (ECE) Exam | Download free PDF with solutions
Detailed Solution for Test: Wave Equation - Question 1
Detailed Solution for Test: Wave Equation - Question 2
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Test: Wave Equation - Question 3
The solution at (x, t) = (2, 1) of the partial differential equation,  subject to initial condition of u(x, 0) = 5x and
subject to initial condition of u(x, 0) = 5x and 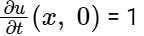
 subject to initial condition of u(x, 0) = 5x and
subject to initial condition of u(x, 0) = 5x and 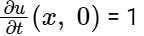
Detailed Solution for Test: Wave Equation - Question 3
Detailed Solution for Test: Wave Equation - Question 4
Test: Wave Equation - Question 5
Consider a function u which depends on position x and time t. The partial differential Equation  is known as the:
is known as the:
Detailed Solution for Test: Wave Equation - Question 5
Test: Wave Equation - Question 6
The solution at x = 1, t = 1 of the partial differential equation, 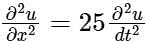 subject to initial condition of
subject to initial condition of  is _____.
is _____.
Detailed Solution for Test: Wave Equation - Question 6
Test: Wave Equation - Question 7
A one-dimensional domain is discretized into N sub-domains of width Dx with node numbers i = 0, 1, 2, 3…………, N. If the time scale is discretized in steps of Dt, the forward-time and centered-space finite difference approximation at ith node and nth time step, for the partial differential equation 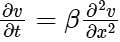 is
is
Detailed Solution for Test: Wave Equation - Question 7
Detailed Solution for Test: Wave Equation - Question 8
Test: Wave Equation - Question 9
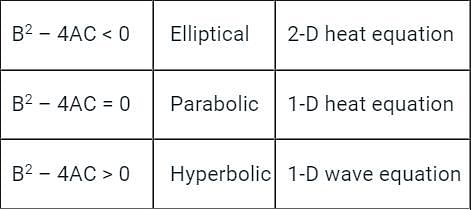
Which of the following represents the steady state behaviour of heat flow in two dimensions x – y?
Detailed Solution for Test: Wave Equation - Question 9
Detailed Solution for Test: Wave Equation - Question 10
Information about Test: Wave Equation Page
In this test you can find the Exam questions for Test: Wave Equation solved & explained in the simplest way possible.
Besides giving Questions and answers for Test: Wave Equation, EduRev gives you an ample number of Online tests for practice
Download as PDF



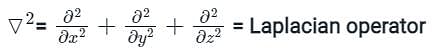



 represents the equation for
represents the equation for




 where -∞ < x < ∞ , t > 0 and c > 0.
where -∞ < x < ∞ , t > 0 and c > 0. where f(x) = initial displacement and g(x) is the initial velocity.
where f(x) = initial displacement and g(x) is the initial velocity.

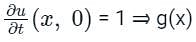








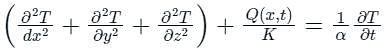





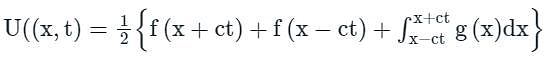


 (using forward time finite difference approximation)
(using forward time finite difference approximation)
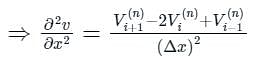
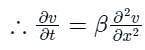 can be represented as
can be represented as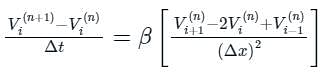
 where c ≠ 0 is known as
where c ≠ 0 is known as










 is the general form of the heat equation, where t is the independent variable time, C is the diffusivity of the medium.
is the general form of the heat equation, where t is the independent variable time, C is the diffusivity of the medium. this is the general form of a wave the equation, where t is the independent variable time, c is a fixed non-negative real coefficient.
this is the general form of a wave the equation, where t is the independent variable time, c is a fixed non-negative real coefficient.














