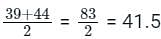Get the App Signup / Login

SSC JE Exam > SSC JE Tests > Test: Averages (औसत) - SSC JE MCQ

Test: Averages (औसत) - SSC JE MCQ

Test Description

10 Questions MCQ Test - Test: Averages (औसत)

Test: Averages (औसत) for SSC JE 2024 is part of SSC JE preparation. The Test: Averages (औसत) questions and answers have been prepared according to the SSC JE exam syllabus.The Test: Averages (औसत) MCQs are made for SSC JE 2024 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests for Test: Averages (औसत) below.

Solutions of Test: Averages (औसत) questions in English are available as part of our course for SSC JE & Test: Averages (औसत) solutions in Hindi for SSC JE course. Download more important topics, notes, lectures and mock test series for SSC JE Exam by signing up for free. Attempt Test: Averages (औसत) | 10 questions in 10 minutes | Mock test for SSC JE preparation | Free important questions MCQ to study for SSC JE Exam | Download free PDF with solutions

Test: Averages (औसत) - Question 1

Save

बारह संख्याओं का औसत 42 है। अंतिम पाँच संख्याओं का औसत 40 है और पहली चार संख्याओं का औसत 44 है। छठवीं संख्या, पाँचवीं संख्या से 6 कम है और सातवीं संख्या से 5 कम है। छठवीं और सातवीं संख्याओं का औसत है:

A.
43.5
B.
45.5
C.
44.5
D.
41.5

Detailed Solution for Test: Averages (औसत) - Question 1

दिए गये आंकड़े:
बारह संख्याओं का औसत = 42
अंतिम पाँच संख्याओं का औसत = 40
पहली चार संख्याओं का औसत = 44
गणना:
बारह संख्याओं का योग = 42 × 12 = 504
अंतिम पाँच संख्याओं का योग = 40 × 5 = 200
पहली चार संख्याओं का योग = 44 × 4 = 176
पाँचवीं, छठवीं और सातवीं संख्या का योग = 504 - (200 + 176) = 128
माना छठवीं संख्या = x
⇒ पाँचवीं संख्या = x + 6
⇒ सातवीं संख्या = x + 5
∴ x + (x + 6) + (x + 5) = 128
⇒ 3x = 117
⇒ x = 39
⇒ छठवीं संख्या = 39
⇒ सातवीं संख्या = 39 + 5 = 44
छठवीं और सातवीं संख्याओं का औसत =
∴ छठवीं और सातवीं संख्याओं का औसत 41.5 है।

Test: Averages (औसत) - Question 2

Save

सात क्रमागत संख्याओं का औसत 49 है। इनमें से सबसे बड़ी संख्या क्या है?

A.
52
B.
47
C.
49
D.
50

Detailed Solution for Test: Averages (औसत) - Question 2

दिया गया है:
सात क्रमागत संख्याओं का औसत 49 है।
प्रयुक्त अवधारणा:
कुल = औसत × तत्वों की संख्या
गणना:
मान लीजिए कि सात क्रमागत संख्याएँ N, (N + 1), (N + 2), ...., (N + 6) हैं।
प्रश्न के अनुसार,
N + (N + 1) + (N + 2) + .... + (N + 6) = 49 × 7
⇒ 7N + (1 + 2 + .... + 6) = 343
⇒ 7N + 21 = 343
⇒ N = (343 - 21)/7
⇒ N = 46
अब, सबसे बड़ी संख्या = 46 + 6 = 52
∴ इनमें से सबसे बड़ी संख्या 52 है।

1 Crore+ students have signed up on EduRev. Have you? Download the App

Test: Averages (औसत) - Question 3

Save

तीन व्यक्तियों P, Q और R की औसत आयु 24 वर्ष है। S समूह में शामिल होता है औसत आयु 30 वर्ष हो जाती है। यदि एक और व्यक्ति T, जो S से 4 वर्ष बड़ा है, समूह में शामिल होता है, तो पांच व्यक्तियों की औसत आयु वर्ष है और S की आयु वर्ष है।

A.
36, 51
B.
40, 52
C.
38, 50
D.
34.4, 48

Detailed Solution for Test: Averages (औसत) - Question 3

माना P, Q, R और S की आयु क्रमशः P, Q, R और S है।
दिया गया है,
⇒ P + Q + R = 24 × 3
⇒ P + Q + R = 72
फिर,
⇒ P + Q + R + S = 30 × 4 = 120
⇒ S = 120 - 72 = 48 वर्ष
S की आयु 48 वर्ष है।
⇒ T = 48 + 4 = 52 वर्ष
पांच व्यक्तियों की कुल आयु = 120 + 52
= 172
5 व्यक्तियों की औसत आयु = 172/5 = 34.4 वर्ष

Test: Averages (औसत) - Question 4

Save

45 संख्याओं का औसत 150 है। बाद में यह पाया जाता है कि एक संख्या 46 को गलती से 91 के रूप में लिखा गया है, तो सही औसत ज्ञात कीजिये।

A.
151
B.
147
C.
149
D.
153

Detailed Solution for Test: Averages (औसत) - Question 4

दिया गया है:
45 संख्याओं का औसत 150 है।
46 को गलती से 91 के रूप में लिखा जाता है।
प्रयुक्त अवधारणा:
औसत = कुल प्रेक्षणों का योग/प्रेक्षणों की कुल संख्या
गणना:
45 संख्याओं का कुल योग = 150 × 45 = 6750
अब, 46 को गलती से 91 के रूप में लिखा जाता है,
आंकड़ों का सही योग = 6750 – (91 – 46) = 6705
तो, आंकड़ों का सही औसत = 6705/45 = 149
∴ सही औसत 149 है।

त्रुटिपूर्ण और वास्तविक संख्या के बीच का अंतर = 91 – 46 = 45
चूँकि वास्तविक संख्या, त्रुटिपूर्ण संख्या से छोटी है।
इसलिए, औसत में कमी होगी = 45/45 = 1
सही औसत = 150 – 1 = 149
∴ सही औसत 149 है।

Test: Averages (औसत) - Question 5

Save

तीन लड़कों की औसत आयु 22 वर्ष है। यदि उनकी आयु का अनुपात 6 : 9 : 7 हो, तो सबसे छोटे लड़के की आयु ज्ञात कीजिए।

A.
8 वर्ष
B.
9 वर्ष
C.
18 वर्ष
D.
16 वर्ष

Detailed Solution for Test: Averages (औसत) - Question 5

दिया गया है:
तीन लड़कों की औसत आयु 22 वर्ष है।
उनकी आयु का अनुपात 6 : 9 : 7 है
प्रयुक्त अवधारणा:
कुल वजन = औसत वजन × लड़कों की संख्या
गणना:
तीन लड़कों की औसत आयु = 22
तीन लड़कों की कुल आयु = 66 वर्ष
माना कि तीन लड़कों की आयु क्रमश: 6a, 9a और 7a है।
तब,
⇒ 6a + 9a + 7a = 66
⇒ 22a = 66
⇒ a = 3
सबसे छोटे लड़के की आयु = 3 × 6
⇒ 18 वर्ष
∴ सबसे छोटे लड़के की आयु 18 वर्ष है।

Test: Averages (औसत) - Question 6

Save

एक संस्था के सभी कर्मचारियों का औसत वेतन 60 रुपये है। 12 अधिकारियों का औसत वेतन 400 रुपये है, शेष का प्रति कर्मचारी औसत वेतन 56 रुपये है। संस्थान में कर्मचारियों की कुल संख्या है

A.
1035
B.
1050
C.
1032
D.
1030

Detailed Solution for Test: Averages (औसत) - Question 6

दिया गया है:
एक संस्थान के सभी कर्मचारियों के प्रति कर्मचारी औसत वेतन = 60 रुपये
12 अधिकारी का औसत वेतन = 400 रुपये
शेष का प्रति कर्मचारी औसत वेतन = 56 रुपये
गणना:
माना कुल कर्मचारियों की संख्या = y
दिए गए के अनुसार,
⇒ 12 × 400 + (y - 12) × 56 = 60y
⇒ 4800 + 56y - 672 = 60y
⇒ 4128 = 4y
⇒ y = 4128/4
⇒ y =1032
∴ संस्थान में कर्मचारियों की कुल संख्या 1032 है।

Test: Averages (औसत) - Question 7

Save

एक स्कूल 6 त्रैमासिक परीक्षाएँ अयोजित करता है। पहली 2 त्रैमासिक परीक्षाओं में एक विद्यार्थी द्वारा प्राप्त किये गए औसत अंक 80 हैं और बाकी परीक्षाओं में विद्यार्थी द्वारा प्राप्त किये गए औसत अंक 140 हैं। सभी परीक्षाओं का औसत ज्ञात कीजिये।

A.
100
B.
140
C.
120
D.
230

Detailed Solution for Test: Averages (औसत) - Question 7

दिया है:
पहली 2 त्रैमासिक परीक्षाओं का औसत = 80
अंतिम 4 परीक्षाओं का औसत = 140
सूत्र:
औसत = सभी प्रेक्षणों का योग/प्रेक्षणों की संख्या
गणना:
पहली 2 त्रैमासिक परीक्षाओं के अंकों का योग = 2 × 80 = 160
अंतिम 4 त्रैमासिक परीक्षाओं के अंकों का योग = 4 × 140 = 560
6 परीक्षाओं में कुल अंक = 160 + 560 = 720
∴ औसत अंक = 720/6 = 120

Test: Averages (औसत) - Question 8

Save

40 संख्याओं का औसत 71 है। यदि संख्या 100 को 140 से बदल दिया जाता है, तो औसत में वृद्धि हुई है।

A.
3
B.
4
C.
2
D.
1

Detailed Solution for Test: Averages (औसत) - Question 8

दिया गया है,
40 संख्याओं का औसत = 71
सूत्र:
औसत = सभी अवलोकनों का योग/सभी अवलोकनों की संख्या
गणना:
40 संख्याओं का योग = 40 × 71 = 2840
40 संख्याओं का नया योग = 2840 – 100 + 140 = 2880
40 संख्याओं का नया औसत = 2880/40 = 72
∴ औसत में वृद्धि = 72 – 71 = 1

नया औसत = पुराना औसत + (संख्या में परिवर्तन/कुल संख्याएँ)
40 संख्याओं का नया औसत = 71 + (140 – 100)/40 = 71 + 1 = 72
∴ औसत में वृद्धि = 72 – 71 = 1

औसत में वृद्धि = संख्या में परिवर्तन/कुल संख्याएँ
= (140 - 100)/40
= 40/40
= 1

Test: Averages (औसत) - Question 9

Save

नौ संख्याओं का औसत 60 है, पहली पाँच संख्याओं का औसत 55 है और अगली तीन संख्याओं का 65 है। नौवीं संख्या, दसवीं संख्या से 10 कम है। तब, दसवीं संख्या है -

A.
80
B.
70
C.
75
D.
85

Detailed Solution for Test: Averages (औसत) - Question 9

दिया गया है:
नौ संख्याओं का औसत = 60
पहली पाँच संख्याओं का औसत = 55 और अगली तीन संख्याओं का औसत = 65
दसवीं संख्या = नौवीं संख्या + 10
प्रयुक्त अवधारणा:
औसत = सभी संख्याओं का कुल योग/(संख्याओं की संख्या)
गणना:
नौ संख्याओं का औसत = 60 × 9 = 540
पहली पाँच संख्याओं का योग = 55 × 5 = 275
अगली तीन संख्याओं का योग = 65 × 3 = 195
∴ नौवीं संख्या = (540 – 275 – 195) = (540 – 470) = 70
∴ दसवीं संख्या = 70 + 10 = 80

हमारे पास 10 संख्याओं का विवरण है लेकिन औसत केवल 9 संख्याओं का ही दिया गया है
10वीं संख्या की गणना करने के लिए, हमारे पास एक संबंध है कि नौवीं संख्या दसवीं संख्या से 10 कम है। तो 9वीं संख्या की गणना करने के बाद, इस संबंध का उपयोग अगली संख्या ज्ञात करने के लिए कीजिए। 10वीं संख्या का औसत मत लीजिए।

Test: Averages (औसत) - Question 10

Save

12 संख्याओं का औसत 15 है। यदि एक संख्या 41 को भी शामिल किया जाता है, तो इन 13 संख्याओं का औसत कितना होगा?

A.
16
B.
18
C.
19
D.
17

Detailed Solution for Test: Averages (औसत) - Question 10

संख्याओं का औसत = संख्यायों का योग/कुल संख्याएँ
पहली 12 संख्यायों का औसत 15 है।
12 संख्याओं का औसत = 15 × 12 = 180
एक नई संख्या 41 को भी शामिल किया जाता है।
13 संख्याओं का औसत = (12 संख्याओं का योग + तेरहवीं संख्या)/13
औसत = (180 + 41)/13 = 221/13 = 17

Information about Test: Averages (औसत) Page

In this test you can find the Exam questions for Test: Averages (औसत) solved & explained in the simplest way possible. Besides giving Questions and answers for Test: Averages (औसत), EduRev gives you an ample number of Online tests for practice

Download as PDF

Join with a free account

Get Instant Access to 1000+ FREE Docs, Videos & Tests

10,000,000

Users

100+

Exams

3,25,000

Docs and Videos

75,000

Tests

I have an EduRev Account • Sign Up with Email

Attempt this test on App!

Get detailed analysis along with solutions of each question.

Open in App

Not Now

Schools

Medical
Non- Medical
Commerce
Humanities
CBSE Class 10
CBSE Class 9
CBSE Class 8
CBSE Class 7
CBSE Class 6
CBSE Class 5
CBSE Class 4
CBSE Class 3
CBSE Class 2
CBSE Class 1

Competitive Examinations

UPSC
NEET
JEE
CLAT
CAT
GMAT
GATE
Railways
SSC
IIT JAM
Defence
Insurance
Teaching
CA Foundation

Technical Exams

GATE
SSC JE
RRB JE
Civil Engineering
Computer Science Engineering
Electrical Engineering
Electronics Engineering
Biotechnology Engineering
Mechanical Engineering
Chemical Engineering

Important Questions for Averages (औसत)

Find all the important questions for Averages (औसत) at EduRev.Get fully prepared for Averages (औसत) with EduRev's comprehensive question bank and test resources. Our platform offers a diverse range of question papers covering various topics within the Averages (औसत) syllabus. Whether you need to review specific subjects or assess your overall readiness, EduRev has you covered. The questions are designed to challenge you and help you gain confidence in tackling the actual exam. Maximize your chances of success by utilizing EduRev's extensive collection of Averages (औसत) resources.

Averages (औसत) MCQs with Answers

Prepare for the Averages (औसत) within the SSC JE exam with comprehensive MCQs and answers at EduRev. Our platform offers a wide range of practice papers, question papers, and mock tests to familiarize you with the exam pattern and syllabus. Access the best books, study materials, and notes curated by toppers to enhance your preparation. Stay updated with the exam date and receive expert preparation tips and paper analysis. Visit EduRev's official website today and access a wealth of videos and coaching resources to excel in your exam.

Online Tests for Averages (औसत)

Practice with a wide array of question papers that follow the exam pattern and syllabus. Our platform offers a user-friendly interface, allowing you to track your progress and identify areas for improvement. Access detailed solutions and explanations for each test to enhance your understanding of concepts. With EduRev's Online Tests, you can build confidence, boost your performance, and ace Averages (औसत) with ease. Join thousands of successful students who have benefited from our trusted online resources.

Education Revolution