Test: Routh-Hurwitz Stability Criteria - Electronics and Communication Engineering (ECE) MCQ
10 Questions MCQ Test - Test: Routh-Hurwitz Stability Criteria
The forward transfer function of a ufb system is 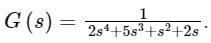 The system will be
The system will be
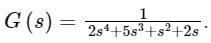 The system will be
The system will beConsider the characteristic equation of a control system given by s3 + (K + 0.5)s2 + 4Ks + 50 = 0. Find the value of the frequency if the system has sustained oscillations for a given K.
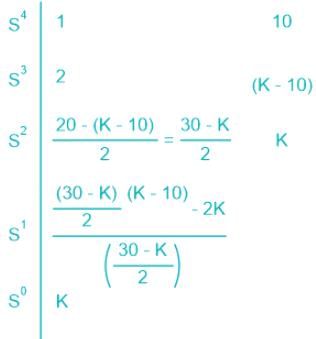
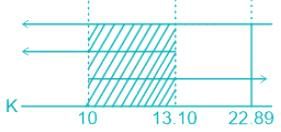
Determine the stability range of k for a feedback control system having characteristic equation -
s4 + 2s3 + 10s2 + (k − 10)s + k = 0
s4 + 2s3 + 10s2 + (k − 10)s + k = 0
Find the number of poles in the right-half plane (RHP) for the system as shown. Is the system stable?

In the formation of Routh-Hurwitz array for a polynomial, all the elements of a row have zero values. This premature termination of the array indicates the presence of
- a pair of real roots with opposite sign
- complex conjugate roots on the imaginary axis
- a pair of complex conjugate roots with opposite real parts
Which of the above statements are correct?
Which of the following is the correct comment on stability based on unknown k for the feedback system with characteristic s4 + 2ks3 + s2 + 5s + 5 = 0?
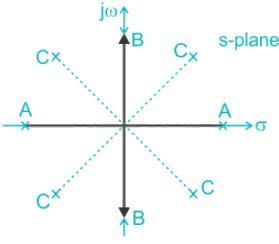
Which one of the following options correctly describes the locations of the roots of the equation s4 + s2 + 1 = 0 on the complex plane?
The number of roots of s3 + 5s2 + 7s + 3 = 0 in the left half of the s-plane is
Consider the characteristic equation of a control system given by s3 + (K + 0.5)s2 + 4Ks + 50 = 0. Find the value of K for the system to have sustained oscillations.
How many roots of characteristic equation P(s) = s4 + s3 + 2s2 + 2s + 3 have (+)ve real part?


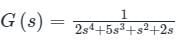


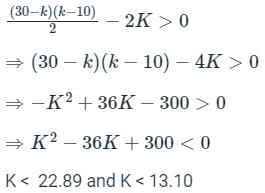
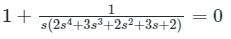
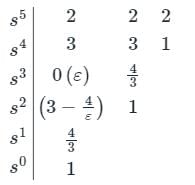


 gives negative values.
gives negative values.