All Courses
Get the App Signup / Login
Sign in Open App
SSC Exam  >  SSC Tests  >  Test: Properties Of Triangle (त्रिभुज के गुण) - SSC MCQ

Test: Properties Of Triangle (त्रिभुज के गुण) - SSC MCQ


Test Description

10 Questions MCQ Test - Test: Properties Of Triangle (त्रिभुज के गुण)

Test: Properties Of Triangle (त्रिभुज के गुण) for SSC 2024 is part of SSC preparation. The Test: Properties Of Triangle (त्रिभुज के गुण) questions and answers have been prepared according to the SSC exam syllabus.The Test: Properties Of Triangle (त्रिभुज के गुण) MCQs are made for SSC 2024 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests for Test: Properties Of Triangle (त्रिभुज के गुण) below.
Solutions of Test: Properties Of Triangle (त्रिभुज के गुण) questions in English are available as part of our course for SSC & Test: Properties Of Triangle (त्रिभुज के गुण) solutions in Hindi for SSC course. Download more important topics, notes, lectures and mock test series for SSC Exam by signing up for free. Attempt Test: Properties Of Triangle (त्रिभुज के गुण) | 10 questions in 10 minutes | Mock test for SSC preparation | Free important questions MCQ to study for SSC Exam | Download free PDF with solutions
Test: Properties Of Triangle (त्रिभुज के गुण) - Question 1
Save

एक त्रिभुज के क्रम अनुसार सभी बहिष्कोणों का योग कितना होता है? 

Detailed Solution for Test: Properties Of Triangle (त्रिभुज के गुण) - Question 1

एक बहिष्कोण (या बाहरी) कोण त्रिभुज की एक भुजा और विस्तारित आसन्न भुजा के बीच का कोण होता है।
त्रिभुज का एक बहिष्कोण सम्मुख आंतरिक कोणों के योग के बराबर होता है। यदि प्रत्येक शीर्ष पर समतुल्य कोण लिया जाता है, तो बहिष्कोण हमेशा 360 डिग्री तक जोड़ा जाता हैं। 

ΔABC पर विचार कीजिए जिसमें ∠A = 1, ∠B = 2 और ∠C = 3
माना A, B और C के बहिष्कोण क्रमशः ∠a, ∠b और ∠c हैं।
याद रखें कि त्रिभुज में कोणों का योग 180° होता है। 
अर्थात ∠1 + ∠2 + ∠3 = 180°
आकृति से, हमारे पास है
∠1 + ∠a = 180°  [रैखिक युग्म]
∠2 + ∠b = 180°  [रैखिक युग्म]
∠3 + ∠c = 180°  [रैखिक युग्म]
उपरोक्त तीन समीकरणों को जोड़ने पर हमें प्राप्त होता है
∠1 + ∠a + ∠2 + ∠b + ∠3 + ∠c = 180° + 180° + 180°
⇒ (∠1 + ∠2 + ∠3) + ∠a + ∠b + ∠c = 540°
⇒ 180°+ ∠a + ∠b + ∠c = 540°
⇒ ∠a + ∠b + ∠c = 540° – 180° = 360°
अत:, त्रिभुज के बहिष्कोणों का योग 360° होता है। 

Test: Properties Of Triangle (त्रिभुज के गुण) - Question 2
Save

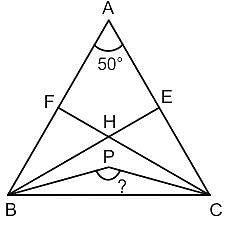
ΔABC में, ∠A = 50°, BE और CF क्रमशः AC और AB पर E और F पर लंबवत हैं। BE और CF, H पर प्रतिच्छेद करते हैं। ∠HBC और ∠HCB के समद्विभाजक P पर प्रतिच्छेद करते हैं। BPC किसके बराबर है?

Detailed Solution for Test: Properties Of Triangle (त्रिभुज के गुण) - Question 2

दिया गया है:
∠A = 50°
BE और CF, AC और AB पर E और F पर लंबवत हैं
प्रयुक्त संकल्पना:
शीर्षाभिमुख कोण = ऊर्ध्वाधर कोण दो सीधी रेखाओं के प्रतिच्छेदन द्वारा निर्मित और एक दूसरे के विपरीत कोणों का एक युग्म होता है।
एक चतुर्भुज के अंतः कोणों का योग 360° होता है।
गणना:
माना ∠HBC और ∠HCB 2θ और 2α है

रेखा-चित्र के अनुसार,
AFHE एक चतुर्भुज है
इसलिए,
∠FHE = 360° - 50° - 90° - 90°
⇒ 130°
∠FHE = ∠BHC [शीर्षाभिमुख कोण]
इसलिए,
∠BHC = 130°
इसलिए,
2θ + 2α = 180° - 130° = 50°
अब,
θ + α = 25°
∠BPC = 180° - 25° = 155° 
∴ ∠BPC, 155° के बराबर  है। 

1 Crore+ students have signed up on EduRev. Have you? Download the App
Test: Properties Of Triangle (त्रिभुज के गुण) - Question 3
Save

किसी त्रिभुज के कोणों का अनुपात 3 : 2 : 4 है I सबसे बड़े और सबसे छोटे कोणों का अंतर है:

Detailed Solution for Test: Properties Of Triangle (त्रिभुज के गुण) - Question 3

दिया गया है:
एक त्रिभुज के कोणों का अनुपात 3 : 2 : 4 होता है।
अवधारणा:
त्रिभुज के आंतरिक कोणों का योग 180° होता है
गणना:
त्रिभुज के कोण 3x, 2x और 4x हैं। 
⇒ अब 3x + 2x + 4x का योग = 180° 
⇒ 9x = 180° 
⇒ x = 20° 
⇒ त्रिभुज के सभी कोण अब इस प्रकार हैं:
⇒ 3x = 60° 
⇒ 2x = 40° 
⇒ 4x = 80° 
⇒ त्रिभुज के सबसे बड़े और सबसे छोटे कोणों का अंतर = 80° - 40° = 40°

Test: Properties Of Triangle (त्रिभुज के गुण) - Question 4
Save

एक समद्विबाहु त्रिभुज का क्षेत्रफल ज्ञात कीजिए जिसका आधार 54 सेमी लंबा है और प्रत्येक समान भुजा 45 सेमी लंबी है।
Detailed Solution for Test: Properties Of Triangle (त्रिभुज के गुण) - Question 4

दिया गया है:
एक समद्विबाहु त्रिभुज का क्षेत्रफल जिसका आधार 54 सेमी लंबा और प्रत्येक समान भुजा 45 सेमी लंबी है।
प्रयुक्त सूत्र:
समद्विबाहु त्रिभुज का क्षेत्रफल = 1/2 × b × √a2 – (b/2)2
गणना:
माना एक समद्विबाहु त्रिभुज की समान भुजाएँ क्रमशः a सेमी और आधार b सेमी हैं।
प्रश्नानुसार
समद्विबाहु त्रिभुज का क्षेत्रफल = 1/2 × b × √[a2 – (b/2)2]
⇒ 1/2 × 54 × √[452 – (54/2)2]
⇒ 27 × √2025 – (27)2
⇒ 27 × √(2025 – 729)
⇒ 27 × √1296
⇒ (27 × 36) सेमी2
⇒ 972 सेमी2
∴ अभीष्ट क्षेत्रफल 972 वर्ग सेमी है।

Test: Properties Of Triangle (त्रिभुज के गुण) - Question 5
Save

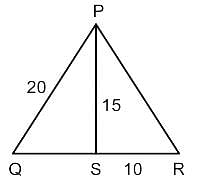
Δ PQR में, PS त्रिभुज की माध्यिका है। QR आधार है। यदि PQ का मान 20 सेमी और PS का मान 15 सेमी और SR का मान 10 सेमी है, तो PR का मान ज्ञात कीजिए।
Detailed Solution for Test: Properties Of Triangle (त्रिभुज के गुण) - Question 5

दिया गया है:
Δ PQR में, PS त्रिभुज की माध्यिका है। QR आधार है।
PQ का मान 20 सेमी और PS का मान 15 सेमी और SR का मान 10 सेमी है।
प्रयुक्त सूत्र:
अपोलोनियस प्रमेय के अनुसार,
PQ2 + PR2 = 2 (Qs2 + PS2)
गणना​:
माना PR = x, PS = माध्यिका, इसलिए QS = SR
प्रमेय के अनुसार,
202 + x2 = 2 (152 + 102)
⇒ 400 + x2 = 2 × 325
⇒ x2. = 650 - 400
⇒ x2 = 250
⇒ x = 5√10 सेमी
PR का मान 5√10 सेमी है।

Test: Properties Of Triangle (त्रिभुज के गुण) - Question 6
Save

यदि एक समबाहु त्रिभुज की परित्रिज्या 13√ 3 सेमी है, तो त्रिभुज का परिमाप ज्ञात कीजिए।
Detailed Solution for Test: Properties Of Triangle (त्रिभुज के गुण) - Question 6

दिया गया है:
एक समबाहु त्रिभुज की परित्रिज्या 13√3 सेमी है।
प्रयुक्त सूत्र:
समबाहु त्रिभुज की परित्रिज्या = a /(√3) [a त्रिभुज की भुजा है]
एक समबाहु त्रिभुज का परिमाप = 3a है।
गणना:
प्रश्न के अनुसार,
a /(√3) = 13√3
⇒ a = 13 × √3 × √3 
⇒ a = 39 सेमी
परिमाप = 3 × 39
⇒ 117 सेमी
त्रिभुज का परिमाप 117 सेमी है।

Test: Properties Of Triangle (त्रिभुज के गुण) - Question 7
Save

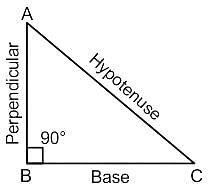
एक समकोण त्रिभुज ABC के लिए निम्नलिखित कथनों को पढ़िए:
(I) एक त्रिभुज में, कोण B 90 डिग्री. का है और इसका क्षेत्रफल 6 से.मी. और 4 से.मी. भुजाओं वाले आयत के क्षेत्रफल के समान है I
(II) कर्ण और आधार के बीच का अंतर 6 से.मी. और कर्ण और लंब का अंतर 3 से.मी. है I
त्रिभुज ABC के कर्ण की माप के लिए दिए गए सही विकल्प को चुनिए I
Detailed Solution for Test: Properties Of Triangle (त्रिभुज के गुण) - Question 7

दिया गया है:
समकोण त्रिभुज ABC का क्षेत्रफल = आयत का क्षेत्रफल
कर्ण - आधार = 6 सेमी
कर्ण - लंब = 3 सेमी
आयत की लंबाई = 6 सेमी
आयत की चौड़ाई = 4 सेमी
गणना:

प्रश्न के अनुसार,
समकोण त्रिभुज ABC में कोण B = 90º
कर्ण - आधार = 6__(i)
कर्ण - लंब = 3___(ii)
(i) और (ii) से हम पाते हैं
लंब - आधार = 3
आइए त्रिक, 9, 12 और 15 लेते हैं
आधार = 9, लंब = 12, और कर्ण = 15
लंब - आधार = 12 - 9 = 3
∴ इस प्रश्न के उत्तर के लिए केवल कथन II पर्याप्त है।

Test: Properties Of Triangle (त्रिभुज के गुण) - Question 8
Save

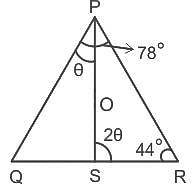
ΔPQR में, भुजा QR पर एक बिंदु S इस प्रकार है कि ∠QPS = 1/2 ∠PSR, ∠QPR = 78° और ∠PRS = 44° है। ∠PSQ की माप क्या है?
Detailed Solution for Test: Properties Of Triangle (त्रिभुज के गुण) - Question 8

दिया गया है:
∠QPS = 1/2 ∠PSR
∠QPR = 78°
∠PRS = 44°
प्रयुक्त अवधारणा:
त्रिभुज के सभी कोणों का योग 180° होता है।
त्रिभुज के एक बाह्य कोण की माप दो विपरीत अंतः कोणों के योग के बराबर होती है।
गणना:

प्रश्नानुसार
∠QPS = 1/2 ∠PSR
माना ∠PSR = 2θ और ∠QPS = θ 
हम जानते हैं कि त्रिभुज के सभी कोणों का योग 180° होता है।
⇒ ∠QPR + ∠PRS + ∠RQP = 180° 
⇒ 78° + 44° + ∠RQP = 180° 
⇒ 122° + ∠RQP = 180° 
⇒ ∠RQP = (180° – 122°)
⇒ ∠RQP = 58° 
अब,
बाह्य कोण ∠PSQ = 2θ 
हम जानते हैं कि त्रिभुज के एक बाह्य कोण की माप दो विपरीत अंतः कोणों के योग के बराबर होती है।
⇒ 2θ = θ + 58°
⇒ (2θ – θ) = 58° 
⇒ θ = 58° 
अब,
∠PSQ का मान = (180° – 2θ)
⇒ (180° – 2 × 58°)
⇒ (180° – 116°)
⇒ 64° 
∴ ∠PSQ का अभीष्ट मान 64° है।

Test: Properties Of Triangle (त्रिभुज के गुण) - Question 9
Save

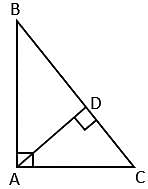
त्रिभुज ABC, A पर समकोणीय है और AD, BC पर लंब है । यदि BD = 7.5 सेमी और DC = 10 सेमी है, तो AD किसके बराबर है ?
Detailed Solution for Test: Properties Of Triangle (त्रिभुज के गुण) - Question 9

दिया गया है:
BD = 7.5 सेमी
DC = 10 सेमी
प्रयुक्त अवधारणा:
ΔABC समकोणीय में, ∠A = 90°
AD, BC पर लंबवत है। 
तो,

AD2 = BD × CD
गणना:
उपरोक्त अवधारणा का उपयोग करने पर,
⇒ AD2 = BD × CD
⇒ AD2 = (7.5 × 10)
⇒ AD2 = 75 सेमी2
⇒ AD = 5√3 सेमी
∴ AD का अभीष्ट मान 5√3 सेमी है।

Test: Properties Of Triangle (त्रिभुज के गुण) - Question 10
Save

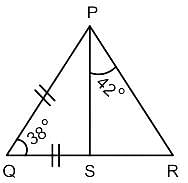
त्रिभुज PQR में, आधार QR पर बिंदु S इस प्रकार है कि ∠PQS = 38° है। यदि ∠SPR का मान = 42° और PQ = SQ है, तो ∠QPS + ∠PRS का मान ज्ञात कीजिए।
Detailed Solution for Test: Properties Of Triangle (त्रिभुज के गुण) - Question 10

दिया गया है:
Δ PQR में, आधार QR पर स्थित बिंदु S है।
∠PQS = 38°. ∠SPR का मान = 42° और PQ = SQ है।

प्रयुक्त अवधारणा:
त्रिभुज के कोणों का योग 180° होता है।
यदि किसी त्रिभुज के सम्मुख कोण बराबर हों, तो सम्मुख भुजाएँ भी बराबर होती हैं।
गणना:
प्रश्नानुसार, 
∠PQS = 38°, तथा  PQ = SQ 
इसलिए, ∠QPS = ∠ QSP
इसलिए, ∠QSP = (180° - 38°) / 2 
⇒ 71°
तथा ∠QPS = 71° ( ∠QPS = ∠ QSP)
इसलिए, ∠ PSR = 180° - 71°
⇒ 109°
पुनः ΔPSR में,  ∠SPR = 42° , ∠ PSR = 109° 
इसलिए, ∠PRS है,
180° - (109° + 42°) 
⇒ 180° - 151°
⇒ 29°
इसलिए, ∠QPS + ∠PRS का योग​ = 71° + 29°
⇒ 100° 
∠QPS + ∠PRS का मान = 100°

Information about Test: Properties Of Triangle (त्रिभुज के गुण) Page
In this test you can find the Exam questions for Test: Properties Of Triangle (त्रिभुज के गुण) solved & explained in the simplest way possible. Besides giving Questions and answers for Test: Properties Of Triangle (त्रिभुज के गुण), EduRev gives you an ample number of Online tests for practice
Download as PDF

Important Questions for Properties Of Triangle (त्रिभुज के गुण)

Find all the important questions for Properties Of Triangle (त्रिभुज के गुण) at EduRev.Get fully prepared for Properties Of Triangle (त्रिभुज के गुण) with EduRev's comprehensive question bank and test resources. Our platform offers a diverse range of question papers covering various topics within the Properties Of Triangle (त्रिभुज के गुण) syllabus. Whether you need to review specific subjects or assess your overall readiness, EduRev has you covered. The questions are designed to challenge you and help you gain confidence in tackling the actual exam. Maximize your chances of success by utilizing EduRev's extensive collection of Properties Of Triangle (त्रिभुज के गुण) resources.

Properties Of Triangle (त्रिभुज के गुण) MCQs with Answers

Prepare for the Properties Of Triangle (त्रिभुज के गुण) within the SSC exam with comprehensive MCQs and answers at EduRev. Our platform offers a wide range of practice papers, question papers, and mock tests to familiarize you with the exam pattern and syllabus. Access the best books, study materials, and notes curated by toppers to enhance your preparation. Stay updated with the exam date and receive expert preparation tips and paper analysis. Visit EduRev's official website today and access a wealth of videos and coaching resources to excel in your exam.

Online Tests for Properties Of Triangle (त्रिभुज के गुण)

Practice with a wide array of question papers that follow the exam pattern and syllabus. Our platform offers a user-friendly interface, allowing you to track your progress and identify areas for improvement. Access detailed solutions and explanations for each test to enhance your understanding of concepts. With EduRev's Online Tests, you can build confidence, boost your performance, and ace Properties Of Triangle (त्रिभुज के गुण) with ease. Join thousands of successful students who have benefited from our trusted online resources.
© EduRev
Education Revolution
Signup to see your scores go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup