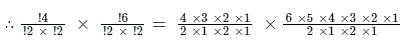Test: Permutation & Combination (क्रमपरिवर्तन और संयोजन) - SSC MCQ
10 Questions MCQ Test - Test: Permutation & Combination (क्रमपरिवर्तन और संयोजन)
शब्द 'TECHNOCRATIC' के अक्षरों को कितने विभिन्न तरीकों से व्यवस्थित किया जा सकता है।
10 लड़के कितने तरीकों से एक वृत्ताकार शैली में खड़े हो सकते हैं?
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
कुल 8 पुरुषों और 10 महिलाओं में से 2 पुरुषों और 3 महिलाओं के एक समूह को कितने तरीकों से चुना जा सकता है?
शब्द 'GEOGRAPHY' के अक्षरों को कितने अलग-अलग तरीकों से व्यवस्थित किया जा सकता है ताकि स्वर हमेशा एकसाथ आयें?
CHRISTMAS शब्द को कितने तरीकों से व्यवस्थित किया जा सकता है ताकि C और M अक्षर कभी एक साथ ना हों?
7 पुरुषों और 6 महिलाओं के समूह से पाँच व्यक्तियों को एक समिति का गठन इस प्रकार किया जाना है; ताकि उस समिति में कम से कम 3 पुरुष हो। ऐसा कितने तरीकों से किया जा सकता है ?
MANAGEMENT शब्द के अक्षरों को कितनी तरह से क्रमबद्ध कर सकते हैं ताकि स्वरों और व्यंजनों की तुलनात्मक स्थिति वैसी ही रहे जैसी MANAGEMENT में है।
शब्द TESTBOOK के अक्षरों का उपयोग करके कितनी व्यवस्थाएं बनाना संभव है जिससे सभी स्वर एकसाथ आये?
शतरंज बोर्ड से सफेद टीम के 5 प्यादे और काले रंग से 4 प्यादे हटा दिए जाने के बाद, एक वर्ग चुना जाता है। वर्ग के खाली होने की प्रायिकता ज्ञात कीजिए।
अंकों 3, 5 और 7 से दो अंकों वाली कितनी संभव संख्याएँ बनायी जा सकती हैं (अंकों के दोहराव की अनुमति है)?